--- /dev/null
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "# Step-53"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "This is a replica of [step-53](https://www.dealii.org/current/doxygen/deal.II/step_53.html) C++ turorial program. However, here we will use the deal.II Python interface to implement the functionality of the original tutorial. \n",
+ "\n",
+ "Not all of the material is replicated since some parts of the original C++ tutorial are only relevant when using C++. Therefore, it is recommended that you first go through the original C++ tutorial to see all the details covered there.\n",
+ "\n",
+ "*This notebook is contributed by Alexander Grayver, 2020*"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "## Python initialization"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Provided the deal.II was compiled with the python wrappers, we can import the module **PyDealII**. Note that it is only a shell and importing it will only allow you to call\n",
+ "```python \n",
+ "help(PyDealII)\n",
+ "``` \n",
+ "**PyDealII** is composed of two libraries: \n",
+ " - **PyDealII.Debug** which uses the debug version of **deal.II**\n",
+ " - **PyDealII.Release** which uses the release version of **deal.II**\n",
+ " \n",
+ "Let's us import the release version of the library and give it the shortname **dealii**"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import PyDealII.Release as dealii"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "In addition, we will import a few widely used python packages"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import matplotlib.pyplot as plt\n",
+ "import matplotlib\n",
+ "import numpy as np\n",
+ "import re\n",
+ "import math\n",
+ "\n",
+ "%matplotlib inline"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "## Introduction"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Partial differential equations for realistic problems are often posed on\n",
+ "domains with complicated geometries. To provide just a few examples, consider\n",
+ "these cases:\n",
+ "- Among the two arguably most important industrial applications for the finite\n",
+ " element method, aerodynamics and more generally fluid dynamics is\n",
+ " one. Computer simulations today are used in the design of every airplane,\n",
+ " car, train and ship. The domain in which the partial differential equation\n",
+ " is posed is, in these cases, the air surrounding the plane with its wings,\n",
+ " flaps and engines; the air surrounding the car with its wheel, wheel wells,\n",
+ " mirrors and, in the case of race cars, all sorts of aerodynamic equipment;\n",
+ " the air surrounding the train with its wheels and gaps between cars. In the\n",
+ " case of ships, the domain is the water surrounding the ship with its rudders\n",
+ " and propellers.\n",
+ "- The other of the two big applications of the finite element method is\n",
+ " structural engineering in which the domains are bridges, airplane nacelles\n",
+ " and wings, and other solid bodies of often complicated shapes.\n",
+ "- Finite element modeling is also often used to describe the generation and\n",
+ " propagation of earthquake waves. In these cases, one needs to accurately\n",
+ " represent the geometry of faults in the Earth crust. Since faults intersect,\n",
+ " dip at angles, and are often not completely straight, domains are frequently\n",
+ " very complex.\n",
+ "One could cite many more examples of complicated geometries in which one wants\n",
+ "to pose and solve a partial differential equation. What this shows is that the\n",
+ "\"real\" world is much more complicated than what we have shown in almost all of\n",
+ "the tutorial programs preceding this one.\n",
+ "\n",
+ "This program is therefore devoted to showing how one deals with complex\n",
+ "geometries using a concrete application. In particular, what it shows is how\n",
+ "we make a mesh fit the domain we want to solve on. On the other hand, what the\n",
+ "program does not show is how to create a coarse for a domain. The process to\n",
+ "arrive at a coarse mesh is called \"mesh generation\" and there are a number of\n",
+ "high-quality programs that do this much better than we could ever\n",
+ "implement. However, deal.II does have the ability to read in meshes in many\n",
+ "formats generated by mesh generators and then make them fit a given shape,\n",
+ "either by deforming a mesh or refining it a number of times until it fits. The\n",
+ "deal.II Frequently Asked Questions page referenced from http://www.dealii.org/\n",
+ "provides resources to mesh generators.\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "### Where geometry and meshes intersect"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Let us assume that you have a complex domain and that you already have a\n",
+ "coarse mesh that somehow represents the general features of the domain. Then\n",
+ "there are two situations in which it is necessary to describe to a deal.II\n",
+ "program the details of your geometry:\n",
+ "\n",
+ "- Mesh refinement: Whenever a cell is refined, it is necessary to introduce\n",
+ " new vertices in the [Triangulation](https://www.dealii.org/current/doxygen/deal.II/classTriangulation.html). \n",
+ " In the simplest case, one assumes that\n",
+ " the objects that make up the [Triangulation](https://www.dealii.org/current/doxygen/deal.II/classTriangulation.html) are straight line segments, a\n",
+ " bi-linear surface or a tri-linear volume. The next vertex is then simply put\n",
+ " into the middle of the old ones. However, for curved boundaries or if we\n",
+ " want to solve a PDE on a curved, lower-dimensional manifold embedded in a\n",
+ " higher-dimensional space, this is insufficient since it will not respect the\n",
+ " actual geometry. We will therefore have to tell [Triangulation](https://www.dealii.org/current/doxygen/deal.II/classTriangulation.html) where to put\n",
+ " new points.\n",
+ "\n",
+ "- Integration: When using higher order finite element methods, it is often\n",
+ " necessary to compute integrals using curved approximations of the boundary,\n",
+ " i.e., describe each edge or face of cells as curves, instead of straight\n",
+ " line segments or bilinear patches. The same is, of course, true when\n",
+ " integrating boundary terms (e.g., inhomogeneous Neumann boundary\n",
+ " conditions). For the purpose of integration, the various [Mapping](https://www.dealii.org/current/doxygen/deal.II/classMapping.html) classes\n",
+ " then provide the transformation from the reference cell to the actual cell.\n",
+ "\n",
+ "In both cases, we need a way to provide information about the geometry of the\n",
+ "domain at the level of an individual cell, its faces and edges. This is where\n",
+ "the Manifold class comes into play. Manifold is an abstract base class that\n",
+ "only defines an interface by which the [Triangulation](https://www.dealii.org/current/doxygen/deal.II/classTriangulation.html) and [Mapping](https://www.dealii.org/current/doxygen/deal.II/classMapping.html) classes can\n",
+ "query geometric information about the domain. Conceptually, [Manifold](https://www.dealii.org/current/doxygen/deal.II/classManifold.html) sees the\n",
+ "world in a way not dissimilar to how the mathematical subdiscipline geometry\n",
+ "sees it: a domain is essentially just a collection of points that is somehow\n",
+ "equipped with the notion of a distance between points so that we can obtain a\n",
+ "point \"in the middle\" of some other points.\n",
+ "\n",
+ "deal.II provides a number of classes that implement the interface provided by\n",
+ "[Manifold](https://www.dealii.org/current/doxygen/deal.II/classManifold.html) for a variety of common geometries. On the other hand, in this\n",
+ "program we will consider only a very common and much simpler case, namely the\n",
+ "situation where (a part of) the domain we want to solve on can be described by\n",
+ "transforming a much simpler domain (we will call this the \"reference domain\").\n",
+ "In the language of mathematics, this means\n",
+ "that the (part of the) domain is a <a\n",
+ "href=\"http://en.wikipedia.org/wiki/Chart_%28topology%29\">chart</a>. Charts are\n",
+ "described by a smooth function that maps from the simpler domain to the chart\n",
+ "(the \"push-forward\" function) and its inverse (the \"pull-back\" function). If\n",
+ "the domain as a whole is not a chart (e.g., the surface of a sphere), then it\n",
+ "can often be described as a collection of charts (e.g., the northern\n",
+ "hemisphere and the southern hemisphere are each charts) and the domain can then\n",
+ "be describe by an <a\n",
+ "href=\"http://en.wikipedia.org/wiki/Atlas_%28topology%29\">atlas</a>.\n",
+ "\n",
+ "If a domain can be decomposed into an atlas, all we need to do is provide the\n",
+ "pull-back and push-forward functions for each of the charts. In deal.II, this\n",
+ "means providing a class derived from [ChartManifold](https://www.dealii.org/current/doxygen/deal.II/classChartManifold.html), and this is precisely what\n",
+ "we will do in this program."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "### The example case"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
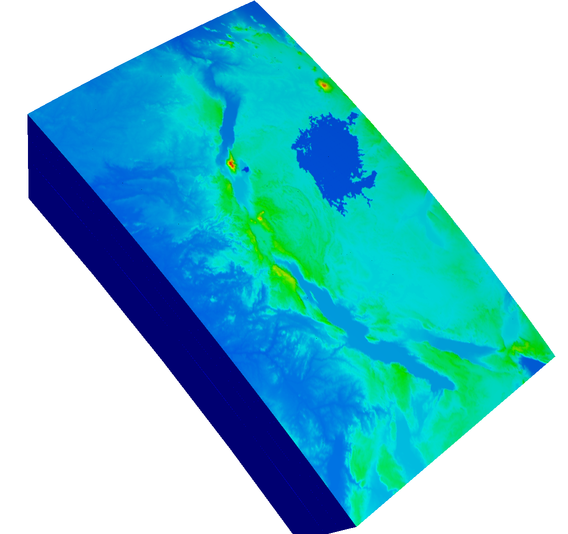
+ "To illustrate how one describes geometries using charts in deal.II, we will consider a case that originates in an application of the [ASPECT](https://aspect.geodynamics.org/) mantle convection code, using a data set provided by D. Sarah Stamps. In the concrete application, we were interested in describing flow in the Earth mantle under the [East African Rift](http://en.wikipedia.org/wiki/East_African_rift), a zone where two continental plates drift apart. Not to beat around the bush, the geometry we want to describe looks like this:\n",
+ "\n",
+ "\n",
+ "In particular, though you cannot see this here, the top surface is not just colored by the elevation but is, in fact, deformed to follow the correct topography. While the actual application is not relevant here, the geometry is. The domain we are interested in is a part of the Earth that ranges from the surface to a depth of 500km, from 26 to 35 degrees East of the Greenwich meridian, and from 5 degrees North of the equator to 10 degrees South.\n",
+ "\n",
+ "This description of the geometry suggests to start with a box\n",
+ "$\\hat U=[26,35]\\times[-10,5]\\times[-500000,0]$ (measured in degrees,\n",
+ "degrees, and meters) and to provide a map $\\varphi$ so\n",
+ "that $\\varphi^{-1}(\\hat U)=\\Omega$ where $\\Omega$ is the domain we\n",
+ "seek. $(\\Omega,\\varphi)$ is then a chart, $\\varphi$ the pull-back operator, and\n",
+ "$\\varphi^{-1}$ the push-forward operator. If we need a point $q$ that is the\n",
+ "\"average\" of other points $q_i\\in\\Omega$, the [ChartManifold](https://www.dealii.org/current/doxygen/deal.II/classChartManifold.html) class then first\n",
+ "applies the pull-back to obtain $\\hat q_i=\\varphi(q_i)$, averages these to a\n",
+ "point $\\hat p$ and then computes $p=\\varphi^{-1}(\\hat p)$.\n",
+ "\n",
+ "Our goal here is therefore to implement a class that describes $\\varphi$ and\n",
+ "$\\varphi^{-1}$. If Earth was a sphere, then this would not be difficult: if we\n",
+ "denote by $(\\hat \\phi,\\hat \\theta,\\hat d)$ the points of $\\hat U$ (i.e.,\n",
+ "longitude counted eastward, latitude counted northward, and elevation relative\n",
+ "to zero depth), then $$\\mathbf x = \\varphi^{-1}(\\hat \\phi,\\hat \\theta,\\hat d)\n",
+ " = (R+\\hat d) (\\cos\\hat \\phi\\cos\\hat \\theta, \\sin\\hat \\phi\\cos\\hat \\theta, \\sin\\hat \\theta)^T$$ provides coordinates in a Cartesian coordinate system, where $R$ is the radius\n",
+ "of the sphere. However, the Earth is not a sphere:\n",
+ "\n",
+ "1. It is flattened at the poles and larger at the equator: the semi-major axis is approximately 22km longer than the semi-minor axis. We will account for this using the [WGS84](http://en.wikipedia.org/wiki/WGS84) reference standard for the Earth shape. The formula used in WGS 84 to obtain a position in Cartesian coordinates from longitude, latitude, and elevation is $$\\mathbf x = \\varphi_\\text{WGS84}^{-1}(\\phi,\\theta,d)\n",
+ " = \\left(\n",
+ " \\begin{array}{c}\n",
+ " (\\bar R(\\theta)+d) \\cos\\phi\\cos\\theta, \\\\\n",
+ " (\\bar R(\\theta)+d) \\sin\\phi\\cos\\theta, \\\\\n",
+ " ((1-e^2)\\bar R(\\theta)+d) \\sin\\theta\n",
+ " \\end{array}\n",
+ " \\right),$$ where $\\bar R(\\theta)=\\frac{R}{\\sqrt{1-(e \\sin\\theta)^2}}$, and radius and ellipticity are given by $R=6378137\\text{m}, e=0.081819190842622$. In this formula, we assume that the arguments to sines and cosines are evaluated in degree, not radians (though we will have to change this assumption in the code).\n",
+ "\n",
+ "2. It has topography in the form of mountains and valleys. We will account for this using real topography data (see below for a description of where this data comes from). Using this data set, we can look up elevations on a latitude-longitude mesh laid over the surface of the Earth. Starting with the box $\\hat U=[26,35]\\times[-10,5]\\times[-500000,0]$, we will therefore first stretch it in vertical direction before handing it off to the WGS 84 function: if $h(\\hat\\phi,\\hat\\theta)$ is the height at longitude $\\hat\\phi$ and latitude $\\hat\\theta$, then we define $$(\\phi,\\theta,d) = \\varphi_\\text{topo}^{-1}(\\hat\\phi,\\hat\\theta,\\hat d)\n",
+ " = \\left(\n",
+ " \\hat\\phi,\n",
+ " \\hat\\theta,\n",
+ " \\hat d + \\frac{\\hat d+500000}{500000}h(\\hat\\phi,\\hat\\theta)\n",
+ " \\right).$$ Using this function, the top surface of the box $\\hat U$ is displaced to the correct topography, the bottom surface remains where it was, and points in between are linearly interpolated."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "### Implementation"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "There are a number of issues we need to address in the program. At the largest scale,\n",
+ "we need to write a class that implements the interface of [FunctionManifold](https://www.dealii.org/current/doxygen/deal.II/classFunctionManifold.html) by using the corresponding Python wrapper. This involves\n",
+ "a function <code>push_forward()</code> that takes a point\n",
+ "in the reference domain $\\hat U$ and transform it into real space using the function\n",
+ "$\\varphi^{-1}$ outlined above, and its inverse function <code>pull_back()</code>\n",
+ "implementing $\\varphi$. \n",
+ "\n",
+ "The transformations we need have two parts: the WGS 84 transformations and the topography\n",
+ "transformation. Consequently, we will implement functions\n",
+ "<code>push_forward_wgs84()</code> and\n",
+ "<code>push_forward_topo()</code> that implement these two pieces, and\n",
+ "corresponding pull back functions.\n",
+ "\n",
+ "The WGS 84 transformation functions are not particularly interesting (even though the\n",
+ "formulas they implement are impressive). The more interesting part is the topography\n",
+ "transformation. Recall that for this, we needed to evaluate the elevation function\n",
+ "$h(\\hat\\phi,\\hat\\theta)$. There is of course no formula for this: Earth is what it is,\n",
+ "the best one can do is look up the altitude from some table. This is, in fact what we\n",
+ "will do.\n",
+ "\n",
+ "The data we use was originally created by the <a\n",
+ "href=\"http://en.wikipedia.org/wiki/Shuttle_Radar_Topography_Mission\">Shuttle\n",
+ "Radar Topography Mission</a>, was downloaded from the US Geologic Survey\n",
+ "(USGS) and processed by D. Sarah Stamps who also wrote the initial version of\n",
+ "the WGS 84 transformation functions. The topography data so processed is\n",
+ "stored in a file <code>topography.txt.gz</code> that, when unpacked\n",
+ "looks like this:"
+ ]
+ },
+ {
+ "cell_type": "raw",
+ "metadata": {},
+ "source": [
+ "6.983333 25.000000 700\n",
+ "6.983333 25.016667 692\n",
+ "6.983333 25.033333 701\n",
+ "6.983333 25.050000 695\n",
+ "6.983333 25.066667 710\n",
+ "6.983333 25.083333 702\n",
+ "...\n",
+ "-11.983333 35.950000 707\n",
+ "-11.983333 35.966667 687\n",
+ "-11.983333 35.983333 659"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "The data is formatted as <code>latitude longitude elevation</code> where the first two\n",
+ "columns are provided in degrees North of the equator and degrees East of the Greenwich\n",
+ "meridian. The final column is given in meters above the WGS 84 zero elevation.\n",
+ "\n",
+ "In the transformation functions, we need to evaluate $h(\\hat\\phi,\\hat\\theta)$ for a given\n",
+ "longitude $\\hat\\phi$ and latitude $\\hat\\theta$. In general, this data point will not be\n",
+ "available and we will have to interpolate between adjacent data points. Fortunately, \n",
+ "widely available scipy library has the functionality for this. \n",
+ "\n",
+ "Having discussed the general outline of how we want to implement things, let us go\n",
+ "to the program and show how it is done in practice."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "## The commented program"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "### Describing topography"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "First, we read in our topography data from the file:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[[ 6.983333 25. 700. ]\n",
+ " [ 6.983333 25.05 695. ]\n",
+ " [ 6.983333 25.1 697. ]\n",
+ " ...\n",
+ " [-11.966667 35.85 722. ]\n",
+ " [-11.966667 35.9 738. ]\n",
+ " [-11.966667 35.95 693. ]]\n"
+ ]
+ }
+ ],
+ "source": [
+ "topo_data = np.loadtxt('topography.txt.gz')\n",
+ "print(topo_data)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Now, create a 2-D triangulation object that would allow us to retrieve a topography value at an arbitrary location within the area. Since we have data on a regular grid with the known size, it is most efficient to use gridded 2-D interpolation:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "from scipy.interpolate import RegularGridInterpolator\n",
+ "\n",
+ "lon = np.linspace(start = np.min(topo_data[:,1]), stop = np.max(topo_data[:,1]), num = 220)\n",
+ "lat = np.linspace(start = np.min(topo_data[:,0]), stop = np.max(topo_data[:,0]), num = 380)\n",
+ "altitude = np.reshape(topo_data[:,2], (380, 220))\n",
+ "\n",
+ "topo_function = RegularGridInterpolator((lat, lon), altitude)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Let us also plot the data to make sure it looks right:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "<matplotlib.colorbar.Colorbar at 0x7f159dd9ef60>"
+ ]
+ },
+ "execution_count": 5,
+ "metadata": {},
+ "output_type": "execute_result"
+ },
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEKCAYAAAAMzhLIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOy9e5wc13Xf+b316urpnkFjZgA2QAACySEJQlQMWRRF23AkW7IjS7akRFJW8dqOdrORnVjxM2tLibOrTeJYcT7OOnESO5Y3cWxH68iyk1CKpay0kmVRFkWCJmSCJCQMSRAYAEPMYKYx/aqu190/7qNuNwYvEbLI5ZzPB5juqupbt25VnefvnCOklGzRFm3RFm3RFl2OvG/0BLZoi7Zoi7bohU1bgmKLtmiLtmiLrkhbgmKLtmiLtmiLrkhbgmKLtmiLtmiLrkhbgmKLtmiLtmiLrkhbgmKLtmiLtmiLrkhbgmKLtmiLtuhFQkIIXwjxqBDi4/r7B4QQZ4QQR/W/NznHvl8IsSiE+IoQ4i85218lhHhM7/uXQghxtfNuCYot2qIt2qIXD/048OTEtv9TSnlI//tDACHEQeBdwMuBNwL/Rgjh6+N/FXgPcLv+98arnXRLUGzRFm3RFr0ISAixB3gz8BvXcPhbgd+VUo6klM8Ai8C9QohdwIyU8otSZVv/FvC2qw0WPI95v+jI316X/u5pTC56qT9IIBDqrwByu91skQgq60zo33iAMdoEIBBI51iJxEcggdLZLgBP/y7XmfGFxDkbY/+bsUu9zR4jJ+S89EEUIJxs+zJQv5D6VpvfSOEcZ/4KEKXaZ65X+tUZRaG/u9vd83vq95RqbGkWR+rziur8ItcrWI6PIUp9Hj0Xe8VU432tJK5WhcBZB3O9Y7pU6cxJVmOKQn03a6znL4TEd6ZcSJBlAEXDroNIppBRrsb1+3i9bXrYEqQcX8ZS2vNOXoo6RtgHUt1CgRQe0veQwrmOINXPSeGsTTFx3e41FuDl6qO+Vl8IQiGI9bhCwKgs6Q/nq9+nU0T9AVIIRFmqa7oBJIVHGQYUUQ3pqfP7owQhJUj9xthHRqjtCKR+6UQpq0dJr5G9CCkRpZp/8dzjq1LKHc9nrm984xvl6urqVY975JFH/ruU8mqa/S8DPwNMT2x/rxDih4AjwE9LKdeBm4EHnWOW9LZMf57cfkV6SQmKYPcMt33kXSRS0iuqlySRklxK5gO1HIZ5d4qCpFQPd6BfwKbnEQhB7HkkZUnLV4wzd85jfm/2m/Fj/VAHerxcSnp6fHOuhu+TlCVZqW9NGREEA3t+gGHhI0SGlCGUkfpnL7I3vi1vqn/ms9leRCCj6jeGighqazCarbZJPZ6XgkirbemsGtNLq3HMZ78Hvv7spZC0x481c/LSapv7XTjbwp5dCzvHr5X89PL7Judhrhmqa/PS8WPN3zJChOv25+Z+7YmisWfo9EjC+e+EaA0AefLdBP2M/GVfguYiZW8BgG1HbuXi/t3MHX8aP8vGpimKAlEUeGXFeEvPQ/o+Uj+P5nsRhqQzM/a4wY5tEC+r87vX5j4D8XL1uYzUPrOt9hyyaLAjTlmo1ex1Hpqa4pMXL/Lks6+t7t3yG4lODWmdPEmQJARJcvm1v07a2LeP1QMHkNEIgNaTS/hZZtfGrIP0fUrPo4wivFTNyytLu200PU3Y79tjs0bDfr/48y979vnOc3V1lSNHjlz1OCHEASGEe+CvSyl/3dn/vcB5KeUjQojXOcf9KvCPUFL9HwG/BPzPXKLFAZXeudn2K9JLSlC42p1h8ACreU7seazmOfNBQFMzdJfhG4qNoBACPI9EHxMIYY8zv2v5vhUgSVnalypHLXyuBYh7DiskDCMFsjQiD9ft762QgOpFNmSEhPN7vLT6rhmUFRp5s2K80hEuLkNNm9XYOEzaMH4zZhkphmIYrNluGJIRFmYe6Wy13wgB89ejYjiuIHw+QsL8/krCwlA5cZ68WV2PEcbmOC9FOPfH/B1mdVa9xCogAKGXkUVr1e9v/ij5qA2rh9X4sw/pI29l9oTiU6V5HuOYIEnwNSM0T6VXlor5OdO1tloYEvb7FKF6XqZWLpK0dlE2omotpxfHhWDmPDv+uGCXANGaVXLMtfaKgsPNJk/OPAHH3wdAfKFL0mqRzswQDQZXWfDrI8P09977swB0F39KCU8qQVod7OGlqRW4RRja9fKzjDJS6xD2+1bY3Egqr228VSnlPVfY/23AW3SwOgZmhBC/I6X8AXOAEOJDwMf11yVgr/P7PcBZvX3PJtuvSC8pQVFKxZxjrc0bDX+PflA6RaEYvsPo3b/gWBsTQiFwxjQvTyIlSVkSex5N37fHumS2SRlS97UFk86OWwSALCPFYIC6X5DLnKwMxrRYKcPKgnAFBYwzN6gEzCTTKyLF0MO16lhjHSTt8XkFvYp5AkydUvtnnrj0fEZwmG2DfeqYyXm6QsN6Sxwm9nwFxbUICXcuruVg5pXOVsJZb5NeSo5iRMbqJBwCWqkA5oOATp6zPnVKXb+h5qJau42DVjhe/M6Pw9PvoXlmZUwTT1otJSyyzDI+6TBGl8n5zmcRx+r3cUwZd9X1GCvBWEuuBeWuQbRmj90RKuUmEB7LWcZCrQaod6dTFIj6KvLmjwKQJX+F1smTVlCZuSWtFnGn87wY8tTaGmXrBEtaYMjv+gQzn3urtQaMIBFFQVAUZI0G5mxmPcOJ8wdJQh7HVqjeCJJSkk9YhF/jOO8H3g+gLYq/K6X8ASHELinlOX3YXwaO6c/3Ax8WQvxzYDcqaP2QlLIQQnSFEPcBXwJ+CPiVq53/pSUokFabN4wdKmug6Xl0isJu7zmM3T3WkKtRISVNR6C4ZI6JHYuip4WS2TcdlHQ3bqkYbOq4fjRDF8I8cJoReTlQjTEsqJibYWRGwzfWg8sIDGOYdOl4KWQT5083+a2ZZ81hOEGvEl6+ZmQyRNSeQ7pWhLFozPmNYAp7SqP100uZFqjtZp7u52sl9/hJoTEp2DYjd22BMOoAkOVTNvySyIJY74+1mxKUQrIniug1E5ayxwF49MKcFdpi7gvIbLv6YW8Bbv4ovdl9sPItANS6XfI4Rvo+02fOWIYWDQZI3x9jvMb94mcZ0vctc2ysrCD9NqO5JvS1a3rmK8rdGC8rQVVMuAXzplISgJW8Rxh1aPq+cpfq92I+COiVJU3fp1tftnPI45jR9DSd/fuZO3ECqBiyYepfC3lpSrS8l/QWtV637DxO7688zsanfoFtp09Xxxm3nxauoCwKP8ugLPE7HdKpKTvfWrd7QwUFUlKWN9ZCmaBfFEIcQhl7J4EfVqeVjwshPgI8gWI5PyqlNBP5W8BvAnXgE/rfFeklJShMMLlTFErLd1xMhsnPC1HFDfKcHMYsgZ7+rbUUvCpIqDQtMbYt1sIgdraZ8/eKwp4LUJqbcc8Y8z/sXaLpDQtf+cT9Pk0d0wDtkgJE/XTlmsqb48zZMDn3HNKxKEBZEDjups3iHYZhhmuKyTjXIGWIEJlzzQW5FGSScQHmpSoWUjhWhRWQDqM2lsck874eIXE9lgRUTNKJQbjnF75icrlUikA9HDquR0FPPwuJ/gtwpN/nddPTBEKwmiun5LfMr3EyTQmEoFP4dI0u0Dqq1kJGMPcIAKPt6nprp/aPTdUwNldNMT5664Zxnr/GygpxJ+TiXhU4t0pBGUFjsRrEdWE68YzY8zjdb0De5OFE3c/jyRot31cMZeqUWoeX/0cuAjz7/cwfe9a60M4fOsS+P/7jyy79tdKdf+nvc0gz+d9++oB6f/Z/lfM3N5l/SIlqryytkDDnd91Loiio6c8mnnEjYykSKIsbE8S3Y0r5R8Af6c8/eIXjfh74+U22HwHuvp5zvqQERaGD2LHn2RgBKBdRrL+7AWxQC2QEA4zHIgKwjN5YKbHn2XFzlBvCxCKsD1vvy2HMr50ZF8CkO0hr7tINBAc9/b0KqK/mOQQ9NVYx8XvzWWuGgGKeebOKBUS98SC3+Y07jmH0rnvMZaaOMBoWm1hYk4IGYEQlLPyeOn8RjY9bRpVgc5n+1ayK6xUQhiZjJm4wu4zGon+531duQI2IysqA0MtVjEpK+5Ltr9XoleXY89UrS/ZHEUtZpp4bvSZ1v2BoXD7mnl08CGGPPI7HrIc8ju1ns90EbI3P3mjWFkfmeUytKQE/2NlU58mcewBKgLixGYCkTdcI+aBnBXsSdTide5BXgXOmTkG0xt6bvsz59Z+3Gn162xfgecqJPI5ZHI24RwuK23ce58RX36WuYbCPwc4hADOnTtnjzdqUjGPZzLzKooAourExiq+/RfHnQi8pQSFEFUDuOYw7l5JVx7XUnAh0u+4oc7zRFmOH0edS0snzMeYfOL9xrYqkLAmAlg509iYfTlfzn/QfO9p1N/dINHQx9jxiUdIp5KWxhEk3kzmHGwgfzVYIJ0Ouj762XDF043ZyjzXuoryJdBFQxs3kbjPf8wnm5F67ocnAsisYrmZVuG6q66XJmA6MxycAvNRaUBVYISP2fFbznANxbO97pygUcEIIOvp+B0KMIeamA8XKu7mvzhUvw87PqJ29BZh9iIJ76bRC/M5OQLmkvDRVDM5xm3hlqeIXnjeGkDL7jOunuZQy2Plyyulz0D3oBNRRwsJFoBmr10VGAdnqt9r1MPvCKYXCXM0Fo5f/Ic/dp6yV6OGf5PlIijKKOPmG18D6k/z7vhZigwNsv/V3WD/292DuIdLeawAVD6l1uwoFptcmSBIKY3FpdBhogZqmJK3W1zy3SZJSXmsw+wVNLylBYfImDKN3GXpTWw09/c8cBxUcFSrUU8v3x+Icxn3lup5cl5axIswYY/ENvc+4jsZgrFAxZaNZGo1Oa9qZZr6Zl5LoeZo4gTQ+5kkkkot4khPM1mXaPmq/SC8VImacoQ7MRmuVMEjal7ptNvutlyrX1WTQ2LWEXBTO10rXinaanJsbtHbdURPwXhn0CDzFEIwVMR8E1s0I2DjYqnZpAgT6WYz1P+Pznw5KuqypoLe5781FFfBufxJOv8NqwiYWkMfx2DY/yxCep1xS5aXuD2t9+D71CxfoR1rwm0B7vAyyB6M2+EozJ2mrtTRCzKyPl1YABf2M7dcgkeU8h7BH/IUfBWDPg9cvJJJWi15brYOfZfBNP6PmquHEeCnrJ/8q7P9Nood/krij4ccaIpw1GnZtTMA6SBJ8sEIDva3W7V73/K5E5SZr/2Kjl5SgAFjP1Utb9wua+qVs+j69srTWhrESEpTGXgWRFRkhMwmbtWgXTU3ftwIIsAKkV5bMBwGLo5E9F2h01cxJ1ntpxRyyJhSzVbARxl8QV7MzmrxLhgEbxJELSQ10LMJVeAwzNZp4NjvO6Ce0abJmFaNwfdqu9XA5IeEyX9elpa9lbE5mjGuJS0xeg6GrCYvN4hHu9Zjtk1aFJtfqXE9jwmDAQq3GsmFQUrIKVtEAJUxW89wqGa710R20oHNICQhQcYukrf56KenKYQDSbBYKgd+fQmr/umGKPur2TuZiXJZCR2h3DlXCwDyPZg2y2WouoOY42Ffl1qCsZSP8ukmbxsrKtc3BIZMbsvTWEfWX/SIAb5ie5sG+JBAp59Brs3FQzevsWyg9zwao/SxjODdHtLExFqQOkoQyisgaDRuT8LOMrNG4oa4nKSV5+jW6P19A9JISFBKpNLU0Bn9YoZscrS+X0mp1hpq+XyGWJlxIY+4kKcndfAkHHptLSWDcW1R5FcYFIWVI6OVk+dQmE4/GGadh0IbpuXEH16du9rkw2El3UBFVwcygB54+ziS5FU4AezLeUWrGO+nHNxZP6gRJDeLJ9Xeba3HHNX7vKyW/XS0mca1B7s0E2Gbng8qF57oCzbF6/yQrztKI43Ld5lHMB4FSRmAsrnQgjq1byk3s3NG4wEqyOJ6/0VxE+H2kYcwAaQ8uvArpl5YZiqJA+D5kmY1XXJXC3vj9dq0FMwfXAk1nVdwEoL6MuPn3kWfebtfk2HDIe3fsUMH7m/8bF16uBNv2p5666lRMbkMRhvR37GB6/69wd1wHlKIVewqeS66ese/Yd5zPPvRGjeSqgtGj6Wm8srxEAARJQtJqEW1sWEFh8ituPOppy6J4UZGUHt3BPACJ37ePUyAE81rLyzWzByVAhCjppg26+uEPvcK6DdzM6qbnEXueggkWlQvCoJtc4bOa5zbIbaGzfkmvkOOwWBh/KSf30YPuwqWuIze/obmorI/ewqXIodBhQC5Fa5cKJhi3GDbLkjYB52wBth+16JdLhIB7DjdJD8bH30xYXI0mhUR4qeZ/VZeYe77NIMGT62OuwTm2Xruo77HPSmbyajKLgjMKQlKWLGcZq3lukVCAzeinuXiJcJbms4ldJG2I1ig3DlK6SgNVzoD0x4EFJjkNgDRVgmThV1Xin7FSDcrNXZ/aWiX086ZySwEM9yE7h2D+AZV5Dgy9lP8SLtEOQ/WcTzuIqqvQaFpVqTjz3TF77/o37PBC7mk07P7lLKMdhpweqLl99uQC7PkonP9O/FP7bTZ6GUqYfwDv3Ler/BGAoolXltZdZ9ZoODdH2O9bIXUjSKGetmIULy4q6uoB16a8sQbceINh4ACB7ytG7ydVvCKbUpqjl1pkixkrKcsxrbBXFDZvA8YztjtFQUu7pgBOpimyaKiXNG9WJv3GwXGI6yT5KRZK6ibBuVrh1CmVBNc5VDHSUVvFFlxGGa2p47zUvuz4TsDZTZibdMWAthj0bzTzsr8z7hrDhIzLadLV5LqhDON13WVeioXuGsvqcjTpZnJQS2PfJ5mhe+5JYeXGJ8w249JzEtgCIVjJBELkbNcPgMk1MJYmqNjUcpbZZE+jeKzmOQEQBgMym97fHre+zPoO29W90EizIOluCvM0PnuXTDyDpXfAvg9Xbk3hxGT0ufbOPcVSmiLLqHI3AX/t5V/g2FBBhE90tYJw5i2c4H7yWV1ayN6rq7ug6hcuAHDTH9/M6eCv8YPf/HErXI/0+zx5cRu7mmvVs9I6qp7v/j7yOKa889+q7Sf+Fjz3Wsq5x6CvLbCdnyHJXk+0sUE0GFihkjUa1k11w2gL9fQiJFFY5iS9FGoXAYMWEjb2YALQSVmylGVjsQjLGLSrYeVy2ihA0COROYmOSRihspSmrAyn2R5vWKGSlYFyKYxuGi91sVmw2ZCMxhPhjJBwNeFlXWdMv9jTu1Qgsdvbrfa5NX9mH6IeDhlmdSUwQAkqYwm447qBZoOKsQgrh7FDhZJxmZwZw1gpbmkRl/m6NOnugcrV5NaDcoXBJi6iK45nvk9aGpMCZnKfk5RG0MOEQ2XQo4MCFnSKwj5bxnowCspkvTED05ajm6o5m9yX+rJi0Iahg1q/wT6oKyYcna2C2sBYDSgT3HXRPmG/j3/+AAXfr6wC99pMxj1KqH3vtm3E29cIxDpLqXIj3V3fxj1TUxyIY4J9SjD8paOnIJ3lmT97Bzte/ktMfeFr89U3H7uF3x79ENykLKjv23eSeHuXR59bqOI3vQU48xYomhQxeF/5YXW90RBe9mElRMwz0lug3PV5km/6DPnD77fB63SuT3SBsdpYz5ckW6inFx+JskIPzT40JgCMG8m1KEyAOinLKnagmcp0rLQOt76TLaGhaW9NEAu1xC3HJbWSCUjarHsp64bhJG3k5ayGSb/9ZvBVUOfuLSim0Tmktk2dqhh1EdE99bZqTC+F5iLhzHEAssEehoZBD53g5WYxCncMl5EZy6FwkvuSdsX0jdZt/OuT1+QKPUPuHNxj3LyKydjM5QLok2SsL2utML7e7vpuEsAes7Ym3WZ6LaUztx5aGdCCcToobcxKFg1WUTWRTGB7GDlac9CDwT6mW1+l6wrXeFnNd/4BK6z6O15H2O+rylxpauGx0vdttrTZFvb7ytKIPaUYGOZ78aDS1J3cmGywh2PRed7WahGAzWNYqNXoFAV31+vs1RbL9+1+io+dUtbxymPvZ1/3a6ux13vlY+o51q7Mj6160Hu5mqt5jtburaDbM09QdrUQlRGcfsd4pr+o7k2+4xz5XvVMTn3lTgY7BXg3EPV0g0p4fKPppSUoiqkqCLx2L1K7d5azoY1PJNo1ANj6TIEQEKgXOEtb4KUWHdXWL0VTQ157wYaNR3QKpS0OCx+S2UsZ52SdoyJSD7sbPIQKdjpZcTVpqxfEkMmDcHHvJmA9bENvgV2H/iFQJQrujyKWUuX+Wo+1puoyJ4MmmZwrqGPcGMnUKXXcYJ9iMG49I+PecYWhC/M15Aa8N2PSrpvIdxj7ZgLM3TaZYWzWZjOUlms5TVobhlyhMjn2pFBzXHMWrqwZelffy+mZkyRiYF2R68kMIlwn9CS5Rt1J7d7qDubHc2DKSN37USWQizAk1H+9CdSNyVY2iXp5HJM1GjD7pTF3EjsesEi37a2v2nn9yPy8FWRGUADcXa8zHwSsaIXoDTMzrO5e5ItfXYCpU9dVssNYO8+9aVFZt6uHK+XHPF/rh6yVQXNR5X9cPDj+TO78DFy4V70DbuyljNSzPf+AEiTAYCeQ11GVLW4MSbkVo3jxkkH6aNN9CMSzxxR0Np1F1J4DFJRWiBw5dIowaleNSZRys7vbYUjuWA4dHaNITH7EhkaIbJbVbMtym6xYh9kM9o2X39CapfW5mryHGhUzNlnReR38AuJldrziF7ivocZ10VqmKOJSmvLYyj7oL4xr65sxyzJSL24ZVUHx3oL6boLYrnZvBJsZS2vBovFUVd/IrK+xXFzIrKv1TxTkswFm91zm+MmquZNW0WReiXt9k0ULzbk3cz255O6/nIB1z+uldFe/GYB1d33M4cY96Y7bXCTUiZa5lKqOlrsm+lkzNZ9c3E2QJIiisBVdR9PTlLs+r+6bKUHuXlfe5A3aHfN7acpvrA7YE0X84927rausHYb0ypJjwyGf1q6c1Txnf63Ggzf/Prt/9W9cM+xU+j7rt90GwNxnCi686zNs3/8R1s/9RXVA1iR+8tXAiHLjO9QU41glDO6+Xz2XRtgl7bFEUGDczdlbqISN+07dMNpCPb34SAqlsRuN0fh48ybrjsndnFoFoFdkyNFNhFNLtj/EjlDS8n3mg4hjSWI1c9N7IhaCprYyclS9qPkgYMUEqQ0ZzV1bNdNTq8Q6mOmWH5f925Q25aJZRKoEXaGZnqfHjZchWcDLBDisodz3Ufbu+QLtsGYDgvM6D8RNEDwQxwT7v8SjJyaq104GT+3AJk6hNWZjEZl4hNGkZx+qXDnmNyY5C9Q+I1yM68q1uAyDNpaDOw9zvGsNuHGXzawE14Vkfr9ZdV03eG9oMn7iavaT1srlBOxm1X3d/Xp9ZNJWwmEyBqWfhVwrNLHnKZehO27rKFy4TbmanIKBpuaRi4ISRQHDNv/X4T/hJ5aWxgpgdnMP8ia/t6rm8MppSa9QsYq3PfUUD9x5px0nl+rdeF1TzeGXz5/n91ZT2v/+RwiS7lhM5Eo0mp4ey4No/f5PEw4G8IrqXGU0Iu50KJwkuuZTPj3eAnf8czj7FruOZE38YaBcazBuRQrnmQx6CpllLJcbQFsWxYuSROXacFEqULmDZp6g27kDgFfe9CxLwQV6peDAlFoqE/gGhWIxny2SKQyttn5PGJKUJR9bnlEPrEEc1Zer82l0Ube2THfbE5WWboLJxk3h9o0AHcQ1zEYzkv4CFD6iqHyiRRiCjJgPgrG+CKAEmQniAxVia/f9cOK9eslSbA8K1y/u+vA3g8wmbcv8bd2iCegmZaQEoYmjoAsaFo3xfhWuIHCFhAthnbTQjOXgCjlznCsEN7NQXOY8+dcwY9e6m8ytMNs3m9PlYLdXoknXnF4POboJgKT2HGF8nqxTWWzilg+Rrvwb6+6xJck1s3bLfhv65fPnmQ8CWzoc4FMXh2OWVa8YkEjJvE5SNcH5XllyPEnYE4b8l46qqNspCvyHPkiQPDJWvtsryysii9buuGPMXWYyznc+9hUAzn9bAd3bsGVLUIIDUMLCf08VuB7NEm1I8tgnvqDjijsjaJyqUHPmOdO1qTjwwSvcjOulLdTTi49EWTGMSd9yX2v4p9+hfLPAydGI+SDgcLNpNfGethxyYEHnSIDSvky84oGeeki7aaxcAEY7Ni+8gaW6WnPq+JiLSPlZoSqbYbR1Q6l6Qb2yhExhzpWbQbfCNBrjzFfYtecz9AqPk078pR2GFt/uNk1azjKVlKhLRTNsK9dWNjvuDhvNKmHlbvPSyq0X9saZunFJuddrtidtRF2Vhpbdu2xSWaxRacOsjvD7lwi6lVFtXACgqrrKogFBr/psaDKRzH0GJnz+26NkLMteZRfPbB40d8cz55kUWGb/pAAzY1yOXKFiXHdeOlY+Q45uIgt61Lc/xh79DJ54+u3IuccZNdQz5SdVuW2DcrK5BlEEMmI5y8bqnC2ORtwS6yrH/kW9DgFLacrpi8rSvvlLCtF1S+s8B+KYT5y8AxIVN6sd/4u0jx8lSBK8sty0Z8ZmVIQhg5ddrDYMduOdLquExvXdNJefJuz3bZyluXSRIEmQvk/rz2qUkXon0ilJkGwQbWzY6w02PNi4nbwp1ftlXLfDtrIozLvHP7jiPK+JJDe8euw3gl6wgkIIcRLooioQ5JPdn4QQAvgXwJuAAfBuKeWfXnFQKSosulvOwbT/vHAvXlqj1NrIerTGerRGIvu2bs2eMLSB7ATsi9UpVA+CQAjuM4lBDQhmv0oAfGwt553zaozfe+JwVTPHkLEwJrVelwpHOGjX0uRLN/nd69zOubUFds0uEgjBoboK1LkuJ9N3YynLOH1Ba/iGkUsdBJSRKiUydKyCYhP3iUgrhqjHGAJ4qdJ6XcbsCAvL0MtIWV+NpxiOVBnseu0i80F0SU+QVzRLm4Ogl5aWH7OcJSRSMixCWw5cZtstY52OVH5BACTh0I5phX6Qs54H450E8+kxAWDiWG5DKrOeidywL9Z6GrNdn88EqOVw76VuLvfv5ciN0ZQRt0+pGMVysEqvKGh6zuu8+35lrRYRZE2kr6yEIgyRuqeFoSBJSMN9rHR3kTTP0tYCueX7NsfIrPlikvN69M0AACAASURBVPAjO3bwG6tLZIM9Fkzxhr2f40OPvBnW7iW+oGIUM2dP2wZL11MWY3Tvr7Fjm0JIdYqCbOmvsNFOx1Bea43vZ/6R1F6Hyb422dXmfEZ4iKIg1pZOEYa6V0eI9CWlp9Ymb26S8Po8STUu+tpgwS8kesEKCk3fIaVcvcy+70F1bbodeA2qd+xrrjycUC/ZsK00XqOppfuUhpzXFe5aa8n16Wd0vEDVZQLlbjJlyd1MWsDCa91ig7mUPNDvA7ESEKCQGMtv1P5qxz0x6UaBCXeTftlK3RL1Gl6+8tU/DnmzQnWZpD/Psxnmxlp6ZqOl4jZr9467kwb7dNDacae4loTbRzvsVcLC+HpnH4KgR5ZPVZZDtr3y15dRFS8KeirAPbrJnmtYRjC9rorqOeVUTM0kN0PeotSkVIzeCCAnLmEsqNjJjneh0lk+pVw7RWOciZt/U6fsPTa1wGLd9AoqBBzA9qiKYxH0lGLRPKt8/4bchMqrCQtNYdShHTbsOiSauZt5hV5OJlK4+X44+W6r/JTeDnXLisIm5GWNBkyd4nvaG3x6o1RF/FDM4VC9zqGpKY7rY5fSlKQsed30NJ/K10DXm/rQl4GkTa0zsDWdoo0Nwn7/uoTExr59cOK1vO0Nqo3Cxy9e5Nz8A9TrK1ZxIG/Crb/O6tQb2fanqqun6cltemEbN5fJFwn7fXKt7JWeh59lBHpemVbsog1I273NFaCvkeRWMPsbTm8FfktKKYEHhRCtibaAl1IZKkhdbW2c0WVNxeDyOrX1nNG0YnzD5dfC3EOcy7GM84hQtXsCIWxjI9ACRLt29rtWhsnLuOAw36V3XBpzMGRcOmZf0awqt07QZFczUAygjCLrs50OSgg2WByVY64bwxyXs8wWrbt9psMJHlKBQBdKWETgRWpuLiMz83LnZlxnRbPC4xsGm87SaiqG02FdwT0nLagyUkJCWyCA7mdeJaNZAIG27PY4JRdcoREIQeAn1fXq4zt6yXpFgZShdWmY4o/WCqFy+0zHG+RyxVoeWa6YSz0cEgifbhpbSyWRUvenyFhP47GYiEXouzEPLyVsPk3seTY+tqlryrRQDXrMBwFHNGppoVajl+es9OfG4yLbj1KvXeTQvR/ki0sacXf6HVBGKtQSq3LaXlnCaJYj/T6Hm03bXrQVBJxMU2LP4480kmlJl87YE4Zw6n+wU4ye+jbCfp9ad8UKiusVEqCYONue4JM6hnEuReU7xOf59u3q/nx+vcdd00Pa83/AZ/cl1Xo9/r8xc7JvLQZQ1kPelKTTs0ytKHeW9H2GMzOUnqcys6eVReFlQictjpdQf160Fcz+upME/h8hhAT+rZTy1yf23wycdr4v6W1jgkII8R7gPQDM71ZCwjA/rTl4mdDBM2Wmmg5ifnYzg5fPqvjFrk8CcLoLp/Om0nqHe605/IynSnrsj6KqQ15R8Nh6COuvHW8tal7mSeZvfPxuPKLwgfol/QRAa0YTD6F1Keixu7qKafan/4pzOz/D/MIfAuN9wE1spVMUFiUyplVtlrx2uWxxUL/1nfwBgyiL1qyrzlTxHav5ZEjDh42bKovWEH7fFm90OwiCEhzGbTQfBHb/vOfZ6zSxJcAKRlNzyaC/EqnLsZjy8b4bp1CuxlgIWlFEp0jsdlClNnQYwCLkrDXjBuIn6ydpIZltHLikqKAlo2AM9tkSL+c2KuH6mJE+k/coXmZY+Hzx1KHKYtt+FJt3oV2vZX8fzD3Eysor+ezUKX5yn0IcvXtujnc9/TTHk8QCNLppzKfOv0JlQQOtReWCUy1W/bEie9dLz7z+9fzBD/wyHzh3jsWRup+vbsbQPMXDvYBjQ+Um3DU14mRa8OTKLeydU5nhp598N9TW6LVfRnN5mdQJnIPAT0obzzAFEqPBQAmL7shuLyPG3avPm25sZrYQwgeOAGeklN8rhJgF/hOwH9UK9a9KKdf1se8H/gbKff9jUsr/rre/iqoV6h8CP64V7suf9yr7v2EkhNgtpTwrhNgJfAr4O1LKP3b2/zfgF6SUD+jv/y/wM1LKRy475i2HJO971PowbVmDuKsEyGgWL5m2D5KpTS99n8HN+mZ7Kcw9oF4yk/gDthOZmH7SMl63ac0n1vIxOC69hSpBDsYZxyXlsSuBBhU2/kramluygVf9HUhnuX2mYxslmZIiuZRWM31mEKjzrx6ucOiGqRkL7HrMcjdzePoJhTQxFPSsn1/KcPx8Zh1cxFHQo944M+baM7WToMpnMb3ITd8QY4UY5u/2ATF9IBIpVSBX36tY94wwlX8NubBld9skdbSlsim01qzntcYoLhf0NtYajNfaco91i/e5LkNTIdastSkV76WqOZXRqJuLCJHR8n3Wl95UzcdUJF75FpuL0VxeZubUqeuOR3RvVn27v/99H2U5y1hKU967c6e1YHIpOZ4kHBkM7FrvjyJOpin3NRp8/ulXq4FMccLWUaWYuHBrc636/fP6c5sKtMHOnep9CZRA4n9pPDIZG71euuuOO+R/+Nf/8qrHvea7v+eaziWE+CngHmBGC4pfBNaklB8UQrwP2C6l/FkhxEHg/wbuBXYDnwbukFIWQoiHgB8HHkQJin8ppbxi3+wXrEUhpTyr/54XQvxn1AW7HU+WACcTjj3A2SsP6tk69EUYQqSRFX6qmHbYU20SE4WYiAYD/Cwj932CdbVN+j4Fh9Xx253s496C8muXEautPwMUasQEj8fQMXlTwV9N/X6oHugi2pxhFD6l5lm+7oNshIVbz0f6PuXL/qt1HU3PHqNXFBye6wMVdNftg2EfAsPAfAcBZFBMZk5uPOJayfR+dtcAxaizfGrz650sn1FGDIc7GAY9Gxw2hfQ6TqzICoYJqyPRGH+3Va05rqljHSZO0StLlQ/juOpMC1PbfMrtYugIIaDqeBfkKpPfkK2FFV0+j2KzddiMTKkWYPvUKuvJzKXHGwj4JArr4sHxfJQpR4DX1saeUwmsD5vVMWv3VqigYDjGbDezeq9E0vf55p/4HQBOjgT3NBrc12jQcXrJHxsOWUpT3j03ZxWw44my9B7s92FOd+PrHLICLNzzB2PP+Up/Ts1bvxNluEYylzL7SGOsQKIoCqY6HQZ7h9d1HVe8RlnesGC2EGIP8GZUH+yf0pvfCrxOf/4PqF7aP6u3/66UcgQ8I4RYBO7VIKEZKeUX9Zi/BbwNePEJCiFEA/CklF39+buBfzhx2P3Ae4UQv4sKYl+8YnwCoFQPc+55tngaKA2j9DwoI7y0wpAbDHoRhlZzUs3XZyhCQZm+hrJ1Qh2czarKm4N9ZAP1AvaaZ1nSmur3tKZ4MDgJKDRVvXaR4dSpKuDr4vF7C+Pa4Wa9pwEvTcfQK5bOvgUaSuNs7zxOEIY2XtJyGNxqnpNLyYI2yfdEOZ996tC4YPBTFb9xrZ9rJWMZmazsmSfsuNNTqwR4KhPZza+4HOrLbB/sY13dClVqT0NFjfBYyjKL1JnXPnZQlkZTo3hscUZ9rAk+G+Zv6n0lZWmD/7mUtl5X0xEqJtbTdvJnVvOcTq7yakS47iCnnFpYk9Dhzep5XS2wrZ+R9Uuq6zL+3RHQQmQEN50nS3aOd7JzYxtunkm0xg/uGXA8UfN9OFqzRQKDp15vTyWKgtH0tEUWXY0W/+YQegvca1yDRcGRfp+763Xe125zWCftPdjrkWirwsDOe0Vhn+cDTV3mf+Yox5KElu/TKzxrOQdAJz5P1lyshN1oFrJZ1l6l4MbR6bvUGMvLyvW8rITu6Jqu5Op0jfDYeSHEEef7r2/ibv9l4GeAaWfbTYbvSSnPaQ8MKDf8g85xxjWf6c+T269IL0hBAdwE/GeFgCUAPiyl/KQQ4kcApJS/hjKZ3gQsouCx/9PVBnVhc15/TtWqRzFcoohSRpSeZ4NxfpbZnruG8ji26Imw30dsqKQn6fv4Z36QpNWivEkxvvX0KOtlxCt2H6Pp+7ae/slgQCIDmtsu8mSkyweUkUJCeem4W2E0C4N9YwJssiKo+7f0PPAvsuPgrwDQ9COFgy9L7otj63Yxvnnb9wBlAVFbg7DH9L7/AkD33F9UfZSzywTfL0d+b9ylMlL9NEJtbRl//q7Io+M/o+phwXhuift7VyvepPCfjXmkswyDHst+v+qDgLIcWr5v4bSgYjMmGx4qFFtLAxOMFQG6KVWeE3see3wfnArDxpow45rmRAu1Gj0NGAAgXCeIOhZVNXYNXsqOeteOkaWtzd1Ul6PN1sasXdC7pEtjGJ8n0MrSvCMAT4+kFdy7ZpY5N2jy24u3Vq7HsIf37FupX7jA/PGHWT1wAFBMdjKpb9IF9czrlWCZ/faf5C83m9zXOMaxRN2fD+7ZQ4AS3g/2+1WXSQ1AWKjV7L1YzXNapjOgFs5Nz+Nu/XwvjkY8s3orAPGX/jqe78P0NLNPPw1Ar90m3fskxMt4Z15POjPS822p4LdWnG4IXXuZ8dUruZ6EEN8LnJdSPiKEeN01jCc22SavsP2K9IIUFFLKp4Fv2mT7rzmfJfCj1zNu6QeIoqCxsmLRQQDp1JRu5OLjpcmmWrr78MSdjkVWuKar8Xv2C3W/i5VvAb9gaf7HyKW06Jz5ILjENQIFT+6+X30c7KvqQpURbHuCsoysye+lonIzed64ye8XsP3omHabS8n+KFJlrk38BfUSLo5Gljl1igKx7cvsiSKLDKK2BpsV0zSM3b/MSzAZy9DWSDZQcMZ64wxQuXTqerhhGVU+ZsP0JpLq3AS2MBhUlXvRDFAIml4wBl/OTRzC90mcpkFQWQW2MyEq2L8nisbbmOY567nHo6ngFc1qzVu+PwbbNdbJfBBwLKkC4jZvRReYBCXA9oQF4I/FSTrhetU/3WX6lyNtOZhe6WZsc50ueGFPFFkrCFQvlPU0VpWMHavkXE9Zlu+8dZHfO28Wskm56/P0dzTZ/lTIttMKT3KlVquL77wTRIq44+8A8HO79rKUptzTaPCuWWUNHdfWACgBbtb9UL1O7HmcTFO7Ng/2++RS0tY9yc21mpI5sefZisjJKz9G/Oj38bLPf942Q5ryPGa/6pO0bqeMlm2W+MzZs7bzHYDjkPua6QY2Lvo24C1CiDcBMTAjhPgd4DmD9hRC7ALMnbqca35Jf57cfkV6QQqKrycZhu8Z7RvtjnIglpN+y6TVuiTwZapvxk5FTK8s8ZLEuqxqZUk6NcX6+fuI2w/RnMDZB1Q+9VxK9taUVtp1i+eBsij6cxbymjdC/OTS9paiKMALof3Jsd4Xph+zgYiCRu84iCBDpl5VN9WCcfXweBHDayW/ikVQROpJMzkZwDBpE84eUeW1ZchwRVfBNT785uIlbhhRe876/8GUgTcVfo1SVDWSiqW0D3ii8yVchjnWYXCi33lSliTOeuVS0vR9FuKQh1dnWRwpQbdHu5wsUooKKm1+e7eOUxnB5eZcmNIvTc3oDHprLP/DrSBwuXiO/usqIFYpcPuyBwFtXVrG3PfTQ5WYKMtI9SNxnr13zjZZqNX4wbZa899eVOVkotN3MdhZMVnzzvhUlkQZRTz99h183zf/Gp/udjl618sBVSrEWFqv08x7OcvoOcLLpdU8JxaCpay678tZNgZWMNdpBIwZJ9h9hKT9ECvl/8GuRxTOxQi15vLyWM5FHseUnsfU+fPcMLpBrVCllO8H3g+gLYq/K6X8ASHEPwP+OvBB/fe/6p/cD3xYCPHPUcHs24GHdDC7K4S4D/gS8EPAr1zt/C8pQSHKUmnhUYSnywoABNoSGE1PM7W2ZoWCKApq3a4KaGsBE21sWGRHrdu9hFlnjYZ1VQ3n5sh3PgsbBzkXrdGcV6bvsSxjTxjaHsoAR4dDVYTt7BuUNm1e1s4hGO5Q9ZtM4G7YpvDbNseiNLEDT2Wlll/+BR4zyI2XfZhgx6NjLiaAQLti3C57h+p1emWp/Pqrh52L0qiYpL15vGSzbZGTC1Jbq+roON3TslPvutRKML0VTIc9sD52qctstGZOqmswmrqTHW2QSb2iUAFpLRiamjl3HO3uQByPoaHcPtbLWcaTw8IKJSlDXt2MePh8m9tnlzgQKwaX6FhG4AgKw8RMfMqsb+77tMOQxdGI+YkaYcaKscK7SOiVg/Ee6kZoTNaQ0vtEuM58ENlx2zo2ZQQXVDWZltLUnuvVMzEtf4blLCGXkX1O7ms0eO+OHXSKwtZvAiBrkh74GGs3H2TqKSX4p86fJ2m1mFpbo7N/PwBvfss/5IcbDRLZ4AO7d/O768raeVurxXdNT5MBww11DXvqEYujkY0/GDqp83xMTM2sr7nP7rE97U51IdJJWfLFDeDOr/DUXmWltx5X2eLto0fH0I/AWGvUG0F/Dq1QPwh8RAjxN1BG0DsBpJSPCyE+AjyBMpJ/VEppJvK3qOCxn+AqgWx4iQkKGea2mqbrSqpfuGAZ/2h62pqojZUVFb+IY6tllFFEkCS2qFptosZ+OjNjtawgSbgwN4vXuZ2yc4gTw4+qg7oHOdFc5ES0xnfsUyZyIATdJ39MMf/nvtP2F/72V/1rjg2HCtViek+YLGkYLzYoIlXYwyCMgLt2PUbLrylNsyzHgnxGs3UT2Qws1NLUqQrlIlJsrX6/UN/zy9TuH+6oUGUjJ+vY9c2beIRIq3IqkxBPqIoCao16Xfc9J1pjOihpOuVIDMN2rQWoNNbhxTttDOjhtaYqK5LsVNaKLrJH0KMeKvizFa3pLA9vKMhpr6yyl9tBQFNDjU32vrEY90cRTc+zxzZ1bTAXYdUpijGGl0xqnxNIsbGAtQlQ+33212q0g4Zl8u0wVPdYCI4OBmOtV2MhODQ1Zbct1Gr0ioJ7pqZo+r4tQWOE3XKW8RurukCCdzPc8pvsbfQ5vQSD16pn+qaZDqurt9J76j18+fs/BEAsqhhpIiV/c6TGnWtP80yqSvXHU+q+HdNzdDv/gSP4nXVxM+pjfb3Gxdr0fQKw9+J0v6HWa7CPxkn1nuSxT5AkrN92G/ULF2zbVdOn44bS16FxkZTyj1DoJqSUF4DXX+a4n0chpCa3HwHuvp5zvqQEBSKn3PbseG8DoD8d4XV3WWFgBMXG7t3EnQ61btdaH1kYks/NAVVnMKDyc546ZUsC+IMBNz2U0GsrYbRa6EzW6WcITnwP+cyIzwa/qbZ5Gl1UXyb+yjeRhCqg+PkT38GOvZ9QL2apczZMcNdtDGS2m8qtmvGu5rnVWg3zAPXiLk80tOnol+1AHMMeFWQ/d+awzTFR66UFg04EvCKluuRCMKyyig3yxI3BZI4f3lgfLoN0cwHc4n1Bj+7sQ3Tzctw94/j1d9S79nqHF+9U+wzSrIzItIUj3baiXsqmAEk9p3NJxHxQxTeM22q/rrq6qOMSVlg4Vo0hk7uyv1bj2HCosv1hTENOpKTplfS8jj0XVLkbxs3U9EJ7j6umWQXPdHbqDPe+dX+ZasFunKzl+3aeh5tNW9fsyGBgXZQGiHFU/BkLtRrv3dnm2LZjjpYf8sZbV/npuX9B50G1etM3TbHtjhlqg5Kzz2yQ3aXQRL2ioLaUkGcl+W3qvh2IY+WS0oLUCIam541ZjIbmdXzCuJoMus2g1ayL0ZSk8VKGc7sA9Y6q25mSx7EtFjh1/vyNDWSjaj1tZWa/6EhUjMaFZGZNylAynJsj7nQsxE8UhYpDdDr0d6gaObVul6DbtaWPJ7t2Sd+3WokqPJZZFJVxSY38fcSdFXrb/apu/u77FcNM2sSdDsnOqpnPyjPvZHr/R7h9pmIYJ9MzDE2TGcP44mWVRe7UZFp57P2s7L6f23cet7WSDMU6M9kwDFOK3HXDnMtmq74M2USA+lopr1fNl1yLIXN6gxh3yrBtc1os+suFkrquF5GqWkMNpyqtyQ/QgmKlX8Fx7X5jgYU9tWYGHupWtp1EXk2UCjdZwk3PY0+kChaal8nAaNV9Si2TNlquG5tazXPV9EdbFma7gfgmUnJS/y7WbXmtNu0wevPXWC/PnPxue21uwcMeKphtmgqBEirGBfnR9XVbgTbW19b0fZurcl+jwRtmZnhnOsXhHU0rvH7uzBl+YudONp5ZozWvrrc1Xyd/bsTophon9ockWji+tTmDmI6IpwICqa7h758/x8nRiERbV+bajDXhItjMnN240FKa0g7DSxMldTZ8fHo7fqYsB5NE62lXtIsiNDD4G0bXjnp6QdNLS1CIomJ6uoc0gNfdRf3CBZJWy1agBGxJAmMhACStFtNnzlhzdbNaS5PwQBP4NgiRUWcaP8toPjNF72ZlFfjH/jZhv8/U2pqKe2jX0nfd+TndcnW7ZfKrec7rpqc5mab0tj/JsXlVNLdTFKrY3tm3jCd0PfednFg9zImgx47b/iOAzSkwDA0UYzCM6smuthaCnsp2NVV3XYz9+iuufe27t6i/bu9sU5jRdT2ZeQ/bkFWaP16q3HFun4ehtqj6C5e6Z8w5zOmTdnUNRvBEa4j6afbXajS9klyaUtodBQLwvCqRzWQjeyn1cEg7rNl1zKXk6HBoGazRyG1Jesc9YnM0HA256XkEKAHjxloWajUSKe24R4fDMc3ahYa2goBPHHtTtb7mOfcUAzXPjlsA0dR0aochS1nGJzc2mA8CG484EMe2P8U/1hnUBko7nAppAf5pJTD/wVKdBiPqu6fw96v35USacnQ4JFnr27gPwJF+nzfMzNDJR3zg1Fm7VqZu15Jj6brPpHvtS2nKUpraBMhssIfTJg8l6HH6tI6x6eTW5M4m3rlvV2N2OjSXl21+lAvrLYviigiu66U/hxjFnwu9tAQFsqqXE/RU2WygbFygH87iZYK0MYCGqh9Dfx9JOE0yN20zkqMNSWf/fvI4pn306KZn2Ux4hI4A8dLUQvAay4pp9W+O2HZafR7OzcEdHwDgU88c4i/f9vjYePujyGZ9u2UlemXJctCF2/6jykYFlYULiikP9rFy+nsAWPF7Ng5ye0u53EzAsOX7hJFiFplIKxeXy6SDHsxpS+B6BIYJfJvMdrUg47GLwb7xrHdTkt21nMx2GO/PbYSOW1fJJTfZTVeBNdBXs44t3+fuel3FFzSUtTe16MBtK7RN0/NYHI3G0FQGUWQQZMv6edgThjb4nTs+d1eguBVoF0cjltLUnte03o21NWG05pNpyrkjP4WpbGuus77ji9qlVQmH2PNAu57MtiP9PomUnF7fqyDHcddex0KtNoYmMlDgI4MBq3nOfS0lFBZumuGfrq/zgV27bCtU08/l586eJSlLC41+/y0ZH1xetjBXc675IGA5y8bqeRklxk2ItP3eazVrbdUbZ6Bxpqowa9bBWI/prHI7Axf37iVrNNj+1FPEnc7Y+3q92eVXpRuEevpG0wu21tPXg8Stf0HygU8rl0e9avxi/f2mPIVmoNZFZRLGANODOuqO8NKU5rJiWtL3rZVxOXLRFVIH1A1qKp2ZoQhD6hcuIH2fC/epmMctB36L+SDg7ji2fthDU1Os5rkt+Wy0RQPJNO4JqEpMHB0MqtLeoDRP95oB5h5iV6wzmfXD3R3MKwtlMmPauPDan1SJgqDW6nqEhl+o5vbGajHz0pmzljqHxl1W7pxBzc3UkTLCwwie2Yeq40y9H7cndP2U+q2bnRz0uKvuW1cGVOgkUJbbhY9/QE13akr5tXd8Ua0FcMtMh7Z24xnkkZ2ClNxdr9ttBunj5jxABSzoaUQUKK3OhTjbnheP/hP1wXHXbd//EStM3NhILqUFMZjfn0xTsq/8BEwvsmPvJ/hNjVoyyKmTOvAMSpP/H48P2NG4oJQRs5aDfVUnRrfMi3l/oDp25okqW9/Q7EPW/Sdqz9ln2giH/bXamDDuFYV1s5nvK5lgb00JNVs6xUDN09nqGUraRM9+E4GGss8fV4CS6TNnxqyJRx754edd62nhZfvkL77v7171uLf/7R9/3uf6etJLy6LwRooheLOXBIJVwb2aYtwG5eOlsO0JxVxqhrk0Id1GOl0j6qq2jaAw2VcTFJOWhnFJmX39fdstAstbeSUA+Z3/gcWkarQDyoWxUKtZ09v6nx0kzWRm64E4ZsnfUF3aoNKsXX98b4FzLEI6y/bm2eq4rFm5hgzp8g5hMCAziYJmLONmuhptlo1trJbCiWeEuiy8gQG7pUTcrnlQ1dCK1tQ/Y1FNLyomOvNEBdFduxfvudeo/JTbfr2qGlpb48lykaCZjzEnY3Gt/8Hfw9PtZ+M0JZ2ZIb14UPUZQd2POFIwUzfpzybmeR6x0fCFIHDiEUZzTwzE16lNZZIAj+te7etHdLE5oS2yqVNWWHWKgiZa4IDtf2EYaa8syTZUVjVn36LWqrlIOwx585fV+e6ae5b5IFBxCi1sDjfVfVm5eHD8Prj9Olxyt7nVhFtHx0uWbBxU9zFeRnopXam7RJYRYTBQcN56BZ7IUYgzs76reY4QcLp706VuyMlWt0A6IxBFiBeGXLj9dnV/k8Qm494okl8H1NM3gl5agsK0Qo2Xx3MVyojSfWD1A+33A+jfM5aAFyQJeXMItTXSmSrIutGK2LjtNrZ9NbHBa28CVTQ2FV3Mr9RN5ONOB7FYWIje7Fe/CsDahX/AHW//BQBy5/d/1O1ad4nRTk2fDBdzHghB4lRbbTVU8H0561RlrV2tUNeZsvm9trmTfslNgLm2DOv3kqWzKhCvxxF3/lOVLHby3ddmXawetgwWUMF4P1UJe56pbjqrLMBh+9J6U0YouPOMdGE746oCdV83Do4zsuYi5exDSjE4+xa7b+p0nTyOeWy6Rv1VKpv4UL3OV3///ZsyEZWRHzG4SzGkpkbt5FISOzWgTKzA9bXfrTOPjycJnYnnZU8UjVkEnaLggV6P7MsfVIgykxVfX4btD6m/+j7JvEnXXK9TfPK0ASXk9Qq+XDTxLr4MsfwXeKx13vZrf1IL7V0zy7aPdiIl0XPHhgAAIABJREFU/+vCkH/2xCwM2uPrOZkTc0kVZGe/KVfj3reaLmDoJpwGPbJojeXac3Yd90eRzTkxdcre1mrR1t0nO8U0v/CMfmd1Xaoxai7iPfcaRjt7jKbO2FpPo+lp6hcuXFK6//nQFurpxUjS27wap3lgc6fZDlBcPKheyJs+B8+9Vh2q69sz0gzJWB+6NLPJsaiGvnLlSLeOFFxax6l/cJFHj/4w9QP/gnu0UFlMEh2AVRh9w3gMJh/GfbuATe5zfb+ZdvnYpLLuXWoNQgdlNNLdAE1/CaONbxysChguvldti5fhlg+xozYiuePX6JrS1GfefOmFmzwMGHuR6+3PMRwqhBkdvb39SdX4CZQAmSwP4roVzDEm18RtENRcrIrvAazdi5+UFI0BU8uFvVe9m7cRdUc0ltcQ9/9vADwGCC7/wg9e859s+YyAmi2FHXueDW6b8uUugCCRkmVtMe7XaCRQNRqansc9upoqwGc/+zN4yTTqDpaUxtgRqarHdeYdldBPZ22fFbfGmV4MVF0W45IaMLr5rLKejZWJavd6X6NBIsOxMu7H8pzbdx/hxNPtS9FhcPWaYKYNsWtteCmkByFbVm4oHYeq+4VGbVV9RJp6TV0hGnueyr5HPeu/dLsRxjexnGXaQlMupqUsI9//szY7vHmXRv29KeDz5/ZW+Upvv/JlXCttoZ5ejOT62F0Ej9OL2D78Jtg6bMP2xwCIlncQ9n36u5p4F15ucy+yxjxZo0HWyMaYved5V0zicV9gA7V1Ibb+2XsobvsDhmfezOdNLGDfh/ki8C37jlq0DFRw10NTUzyoK212ioIsbXG66BF6lVBp+j7b4w3NvBTTynQlVpoOfDjUjHXS92+gsrGzjoN9yKJBs5aT5Dnh7o+rQzcOjifdmXGNgE5nbfBxeO67qvthApLxsnJVPPWecZeh2/nPhdCaeEoRjRWzsx36zLapU4QXtlO/MH5/mmdWuB7KGg1VkjtTkOZWI2VxNGJ/FLFQq1lGb+oVuQzOZGQ3fZ9P61wcUDDUpu+zJwz56c+9FYBgo4b0qxLzni5XQud2baFm+B2lYfvZxcvO18TFkr3abjQCVLufzD2Wo5t4kOfG6lgZV2YgxHh58uspYAiXtzb6+6xbE2DYOsr25lkOxLEty2HWy8163ww2bI5diGN6RWHbuS7UapxMU1V/LQwtTHg1z3nlTc8StNV1PXxtV3JlkvJaq8e+oOmlJyigeqBd68IEtE1bVFCaqYyIT2+3sQTpKwy2PwwIkr5FSYT9vmpSPzVVMfm+2l9G0VUtC5eEA9Hb8fjjrGXfR3rgY9UB6Sy0jvLFpw/zHQt/UsEds8wGuS+5XqpApvmcA7mDRiFvVp3PTBC4c6gSnC4zdsuiu2WuH/0lntn+mGLspgxIGanyIxsHKyZthISxKnQ+yfT+jyiETOcvILZ9Wa15tl25Kowl4Ts+Z/N7cy+NxeHmSoCyksLe+P0Nekh//gp34tpoNFdCvMwtTYWQmg9iCwd1c1KMFbEniqx1aJA/n97Y0MUM1f1ZyjLmdV5FdOY2dblepVi4fUgM+Vl2zdDOZO/6OCjAuOtgzIUkiwaJGIBTZHKPdvFsn/9T1jv6N66bb1KZuBxdrmy9IyjwVMHCXjmw7i+zTi7yy+1TbgoDAiQ68dEVIKYECCglywobz6PlCPYbQZIti+LFSa6AcK0LqJAvE8lVyZ0R8VdUMdsgSfCzjLjTsY3cQVkBtW7Xwl5BFUpLWi2k79NcXr4uYWGOFb7P/PHjjM58M/0dGrY438R77P0AfO7Zt1LueBSA6YV/R4ByN1nUx8ZBFTvQPl6bM6G1wnMbbdVHGZSAMGgm8+K3jiqf9YV7L3XlmEY8OoDKxYMwta9CF5mg9k2fU8cd+KCKXUCFhvGVwNi+/yNAVcytvedpVnV5kKQ2oFP/r6xc1MLHBKihsvqMxeOnkEUVCsowHDNXk2Cn940Of5LR8hupLX7zJcmTVyKTWzPamUD7fvZuP82humL+S1lG4FyLteI8j0NTU8wHAb+zpuZlCt7dMzVFIIRN5EvKkt/+0++l9vTdeIVac6MnT3Y3vBqkc7CzrtxKZj3SWXXPjAKgO9nJoqGKL2oXmtzETWugxD3dxGm6pWJp3eZiVZ9rsyKGk5ZGEY0LKldoFFXxSNJZaC6Sz33BZrMbi8JksxvaE0UciOOxuJ2J48WeZ+/HnjBkWbsA3X7rBjhgXIWfutKiXiNtBbNflOSUYncFgtt5bDI4p01qwxiSnYKZk328NFXd8kxhQW1FuMgnk5k9imMFhdVaZK3bvWZkhdEc407HMrLy7A7gOGu33qrGOq+SoboX/jXTr/lRBXV82YfVAK2j4KXIbDtDYDpW7o3VPEee/mvq+gwTWT2sqtS2TlSM99nvrwLJBjlkxs2bShAZoWJcVNu1NdLQyYRL30oRexbVAozDI6M1m9h2T0PVnjIZy6D84vtrNRb9JZLWh1X5a1BWSG9BMT0dgLV5MpNJd2a7cbMYWn4jDPZRhCGX1i3dnHo371BNqgCCHrfvPM6eqDZWRt708Xa13rvrddsTw7hyFnSs6YC2WD90WgnH2oM/xlSWwSadtI1YuJqASFotyr2fqEqfgBIUoY6tGSTbxkHkzBM2qdAoExmAl+oe4Dp2IgTLOnFwjxOozyMJ+/94LB+lUxRka/eocd0YEoA3IUC8XuUuBOfvLOSHkL0FzulrWN3zB7ZelrHWDJN/oNeznQxhPEnProvO2TAWipu4ONkB8XnTVjD7RUhlMJ4PYDQf41+N1mD9EP5QF87Tgel8ZmRN+vhMpQV5ZUlmyivrCrNuAo/peWGsA1MewPSSAMb6c1+JRFEQmNhHliF9n9bJk9aiAaBxhu6j/0Rp2W78BRWYVEliusOd77NeW4aB09qyjAj7fUbenTD9jNo2dQr/wq2K0ZvjQGmD2Syc+64KfWOgqmfeQdDP7NyKRleBAjqHYOFfqWNXD1eM28HaL6XKt24qhoJiTr2i4FC9zlKW0d6uLKvFqX9Hd+1uJay0VVOfU6Wkh/2bq25yoO77yAnGA+H8n6i4zLBNPjOCa2vOBoXP9E7VPGx/FHHPVHMs5wKwZSRcpmUsutjzbFkPAz01iB0e/3EA/GyNy9G1JIUNZmfVPewuKEXAuBLzJtBWbiEjRA3SKF6mHg7JDZ/0UtURz3HbuDGKQAgrzBPdV6TjZH63fB92PKoExuq3jgsLo6i5gjxpV61YXcizsQJ1kDk79S6S/R+hV5ZWwBoY77KpNjuxRrmUdlvseXTy3FpzbikUUyvqRpFkS1C8CMmrBIRBXoBiehrL76U1gkRp7n6WMZoraZxJEYVyCdj4gxYctn7T9LQtDGiEgLFCijAkSBIrMPI4Vr0rHFeUWybkai4QY2V4cUzuedVv41OQ6YQyEx/QAUcZrZHLqgdBLqUy9wf7CPq6OU8jRBQjosGA1Nem/80fpdi4k6g7IG1lKtgI6hwzT8DcLMEZ1WcgZx8UKhAfJAlJU3OcV/wcPPaP1Ro/+T61ra6FxIV71X3QMYrm7Ic5OhhYRgqKGeeoh3Wsh4QQrO48ztL2xxguK1RasOuPVdbxzDLnNqgEZnMRRvdWxQlBMa8ygu1HaT529dwP6fuq5tcr/nfaGkDQ1sHQTTvlOTkYUOW7uNZSywkUv+pIes2tRC9HA90IiMaZCjactCu3kEl2q1WCqL79MYajbYTBgKSsmkAZcutYGY3bMFjDVE0Zdze5D1Q8oVMU4zEQqOJbbtJd3qzK0evndtfMsipMCZWV2P6kLVZotP92GHJ0MFD3I4rGK/Y6cwTlmjVWa+4kMBoLxYBDbghJ/n+Rmf0SExTlmDvJoh2TNlF3RDo1hZdWjYe8skS3PhhzFZlS5aZooLt/ND1ttyWtli1V7meZZeh5HJM1GkQbG1aoxJ0OWaOBl6aM2m0rgIIkuaybKtrYsGMD9MG2qix1GQYbpF89rHIjTDwhaSsBuf83yXUl18YTStsuo0gnIEK5fq8K0rcyGmdS+ruUphc982rSqdfCLb9N/LhyfeVJJQCTVgtq2g23cli5wtburWIGZVTFPeY+YxnGw8/cCzseoFcrra94Nc9p+r4qpe24O0w71+Us42j4J+qySqXFd0BpocaCWD2sLJp6Vf8pevztVrhfC/W/9aMwdYpvaaXsr6l7afpLGJcSVPWJjNbt5kGs5rnK2HaY0f/H3rtHyXVedaK/77zq1KNbpX5ILaslt+xWLMvyRCHGOAtn4RiHcXKzINwxswIXuL6EyZBFGJhLuAGGNWYRuCtwuRCG5xhmJsAAmSRMMiaTx3VIDBbEseVYsWVLsdpWp9VSl/pZ6nqdOq/v/vF9+zv7nK6WWk57Yo2919JS9alTp845VbX3t/f+7d/vsU4HP/tChMo//DSywtLWLajXkd74F+recip6CpKTn8goWdYPGTla6mM5QmC83EIsLd17yK7DEVlph65hwnVR19TqNZZpTLgu5sPQlHQAmOtdHj5ttDWE3VGU7peymSVzvq1p1V/SpaeFxr0qaKzenqGszt6PJQBLBz6CpzQS8JP1E9g3uoxDWg6VqNIpgHAGg+U4NqinmobVAqoMuO2lp9cyimvRRB5eSagMESLU/QNilASARPcYEteFXTySLitRecUKQ6Sel6PpIB1hkSRIXNfMVySuC1cjokIdVC7t2wev20Wsm+FUpop9X2UPBa781LIMAyYFttHHhtEfshHUQ/hay7QbvlHRfF/3kHKU3/ghAIDdqWSBbvffAVDJQu1sAm993RyzM+Qh3nMGw8+OwgpDVBbV9XX39WC1fKSNexH76rpKrRZ6o6MQrot4Zyur47enVdmHy5smniqJXPeQchbUY0g9CBGhZvlmJci5kzhH0aTrmtUhQRznw5CxocZ4JtXOpTIHVOZgnfoppmB25SBBn2/32z8J+A3sqbRxtFLPUVrQcB1ZkKY4UqmYAUnKJJq6efrjY2NG3+EDX/gxoD+CyuJAYvNNrXvT1xX9CKDIESlLpvtIYlPtaaBxLyLGbxXFFRysxIg9zWOVCMMQS/0VIGOwpQwCUAGjzeg/OKNrW2cUtI0CJwXN2FEZwUJ7t1oYuG0g0t8HyiwSTQPP4bPd/ep7Q7/d+gn1jw3HYv4+nGvO4I5/8jl8qtk0UNh7hoYwXSphzHGMcBJ9HpRV0LWdSBK8f/du89rtMClfQz29bCaE2AfgzwBMQC2xHpRS/k5hn7ugZP90MR3/VUr5K1c8OJ8OpVTWbQNlRUbH+ZdopR5Vq5D6y0MDTAAQaH4m2tftqCY3zwDCSgXh8DBSyzLOv7s3AcJxeK1+LntZ37cb9RfOwet2c0HBCkNE1apBVPWHhlCfnTVC8LxmbUdRLgsZefFFpJaFZvluVF+smRKa1GU3adtIaKXW3Y/U26FIDPV51Z8FUk/Rr/eHhsz1VmcTBPUEGH4OYUexcsa+j/jGv82mo6lMRbQaI8eyFT7RN6wdBcaPYafWdzjk+whkxegQAIoam+gwOEqF0C9cx4Gop0/0erhraAhTWj52PorwFOauWuaye9PX1YPmUZRHn8SdtR2GOJHOgWre5rwcB0fKZRxrtxXMlVGKH+928cB/+bmsdAnAjrYWJFLLQnDzE+q7uyvLwlBu5PU6gGywkBr7FCicNm6uJjjVquCghvPSSnoWWaMXgNFVn2Y8S/NRhLptY1nX+Mnp3lGt4kQUIUhT8xkVsywK8EFlGUFZzaoY2dXh5xRgoqOYAYiw01xLdz+jfLlb9caA3HQ5ggl8/O+OAgd/D35JHf+RVgufWFvDkXLZlATHHAfzUYSmBkmQNZME75+fNzre22GvoZ5eXosB/KyU8qtCiCEATwohHpZSPlfY71Ep5Tuu6sipZ4j9TJav9Q+sSORmGKhcxMVMHABSN5Z5lqB6GQrdRNuI9x5QgcAElfUhJPUGnKWyEUkqtVqov3AO4fAw/GbT9C+IPLAYwEwz3PPQ1QGEgkuRU9+OIlRfVLrfhgI9itAbHUUy+mJuTsJbF7msiALP4ncmcBbGEY+qclL/hgdhfe0BIK4hrapt6R5d/yZkFEc4eau4uWzjVKgc1p6RGSyc90yfZGJUaVCf1lPnfCiN4IyAqjNz4jyi2KagQoI2bebwAFXeqX32lwZ9IzY1ErQBAPeGP8E7dtQ3KNI5QqjgxF4XS2nYVX0hzAr1s8/dg9Lzd8CLrk7zwHzHpp5Xn5Vmy3VHjgNQDnmpX1LOlBPw0WLIWzVaJmeCFDP9GHASzIYZzYuvs4Y260fUbBsolE1qukFfVJ2jz6KZJIa88s6aavIf73RM8xjQdPhaWnZGnASghaVqMyrozd+XvWHqKZi1nWQzS61uRqrJtEmssIRUeMDs/TjVOqa2D80AcQ2PxjPYV1KZw3IQKLgsK20Cqkz1WBDgo6ubAwmu3ran9CSE8AH8PdTawgHwCSnlA0KIXwbwLwDQlOgvSik/o1/zCwDeDVVk/1dSys/r7W9EJoX6GQA/La/ADvuKDBRSygUAC/pxSwhxCsBeKP3Xb8IE4LZh9xwkTmxkPJ0gQFwdQer1Yfcc00uQbICOfqxclEgkCUr671ILWZlJO+7OxAhKza5CEg0NGQ4Zv9lEx90LkSwZ9lkrTdEfGjJTt5Q9+M0moJvhZF63a0pS/JwsTVBHw3+AcjJeEJgmKQWBWMu7VhZLCOpvMcdJvTSH3KJA6Z8dQuqx+vnq7Uj3/q3KGghRQ//TypbPozhtnFo6YFa2zSTBkG48n108lOlfBAfg7DyTk8WkVd+URrXU2Gqe9BX4KradJLhneBixlPjwxYsAgO7fPHBZCo6itSd3ALu/CLFHDTpOeiUca7fxjh07MK9XzmRNXXoyMyCui9l+HzUN4fz8w4qrq9JsYhDcdTMLKxXEBx7NmHVTLyNQrJ8wPZxmkqi6P+e8SnUZKq7h5qEexhxqUEcAPAXfTbP+QpAotbhDvm/ue1svmEipD1DlpHkdFEgpD8hQR/PNJo7rbPREt4soddSMhnSBWAdeTZdzsreEoxq0cDII4FqxopW57qE8IrF5VM/kqHueuEob3m82zSJOSROHEIkD9HZBrHyfuY9x1QWqMzhHDfzaDFA/gUbUVvoger+T+jdzond1ZcDL2vY1s/sA7pZStoUQLoBjQgjSuv5tKeVv8p2FEIcBvAvALQCuA/AFIcTrtG72HwJ4D4DHoALFvbiCbvYrMlBwE0JMAXgDgK8MePpNQoivAbgA4P1SymcH7JNZagPhCJKqmt6lFYq0bUMHkZRDEGY8hirrxKMrhoIiTCpGWxsAQI3kCVVuKS1m2Qc1hBPXVQN6+sdGqnfF8lJ5ZcWs+vlzdhRBMr4eK00R1OuqDBaG8PW+POMwQURnPnSd9JjmQKRtmyCSep7qvViWCWqkDe43m2jeuC/r6wQTyunveC4rgbSngeHnUC4v5Wr2vhWgFYYQ5XPGybfae7GzdgGxlHjL5Iv40vwNaufKnJH05OUdkses2bbRIJgJAgMvNRBUzZRLq3iCT3bueAi1fxjAOcWMMoiwUgHGHwYu3g1JU+0H/sbg9DlFBNW3SR0QAL6wvm40qf/s4x+Al6ybz2dLw3FAnneJZGN9xYN0a0VlTTN9FRRIhCquLJsftBGxCiZwKm7nMg3Xa+rZCHUdrVifU1rGibRjUE/jrtI6OR0EhsGYCyARbBlQQeF4twvfsszro0jNJxl6+wJku5d6+HKfpsGZciGHx5LImNM2BYAUADr7EQd1k3n7zaYJIEXzuoBojCBxlSZ6MHo7sHg3ousewhrPgPU8FWUe5y77SW3Ntgseq1f8BBtz9b/LZQHfB+CjUso+gLNCiBkAtwshZgEMSym/DABCiD8D8E5cy4FCCFED8NcAfkZKWew8fhXA9TrCvh3ApwAcHHCM90BFT2B0Uv34dJ+CHKuiJ4hVDdQLDWw2Jc0KVuONMQ1p15H4Fuwga3xXG6u66ZyR/FETm0jZKFBQI5o3yWPfR1CvGxqGIu+TFYYAe723vr4BZivYfAb9YESSQKapWXkRmirVHFRRtWpKVUmU56kCkMtMnE6EUku9V2/0DUj9FvxFieCA/klp9tne5CdQdnvGiQLQOhduVq7Q95PKFT8wpfokvmXho6vIrdCBrGn8qWYzRwR3z/CwCSSAyj7mtfgNoYwAXDFIABks2e10ELfuQP/QF5VeBoBzKzcC3iom6upraEjy9Hk24tgI9txZq+FYu41zf/vrsOy84xoUJqw0VQGiMpfBVkl4qTqD8eseNdfrCEUsuLB82GQPLZ69kZGjrczl2VitEFGwKxsy1dtof+lkvbulnsoEhYjM/T1aLuO4RhE5XB8iTXFbpaKmp1M/O4fioB1dGw1ncsgssJEtIfEAOicePKpzSHeuItXU8PHwBKxgyGTTVD6m3zgnRqwspUjcYfT79wMHPpKH6Lancc78/Xsbz/1qTWKrgWJMCHGc/f2glPJBvoMQwgbwJIBpAL8vpfyKEOJtAN4nhPhRAMehSvZrUBWYx9jL5/W2SD8ubr+svWIDhU6v/hrAX0gp/2vxeR44pJSfEUL8gRBiTEq5XNjvQQAPAoC44Yg0ynZ2G0iUGpaVpuoHbCcZHxAAgA39EKldaRUJRlT24brG8Saui2Cvh0oj4+CRvm/gl1aawtYr99j3AS3sbobSXBd2FKEzPo5Sq5ULFGRm7sLzjKNPPc8EhUQHCso06L2kbZsSmsk0dFO+mH0AKiMhFBiQQX7V4KFyAqkr4S9KeN0u5NyU2m9C39fmUfScNpwRVX+mMgVHywx5gSJ2Y5O1APBYu40xx8FCCJM5TJVKCk6q69wOkSBaFj66uooxx8H9Y4qzabbfx+fW15WUqW3jt1+sFT/JTY3uQ+p5KmOMa8DZ+9WTex/CzsoyYs2kyuVjAaWN4Ot7FkuJs+t12LaNFDDZGf8suXX3dgDvvHKKnDyxMgd39yNY6qvjjpf68C0LC4tH85xVVoih2gW0mq/Ls7HyYEDOj+DhnBSTG803AIC3ij0eEKS2CfCzYYhJzzOltZMs8510XZWpFPXLqWTGz40TQgJ5nikONLFDQLbzAacoogUApVWkAOKksqHPSGazjFwkCcSyi0C+BzisMDDl8pLSoaeZk20wiS0r3C1fSbhIl42OCiHqAD4phDgCVUb6IFR28UEA/y+AH0OOhoKdzubbL2uvyEAhhBAA/gOAU1LK39pknwkAF6WUUghxO1QefXnloMTPVN2kZxATaerB7jmQtkAKtrpI9ZfZZque/ohqmukyQndC//hdxSPUtffDWVNlKTuK0Nq7F7VGA7Hn5XoJFvINbujGuBMEuSY4GDzXaPsmCewkUX0P5tSdIBg4F8BLWaahDtXQ5sN9ieua/gitxCgTsaMIzvoQoqr6cVYbK6Z3Y66BBqW0RkQrVCl97PYM9r5osSa+o6AwG+oVr7eaUW5riotZDX0lp3XEtrGcJDjk+6Y0QoR7p4MAp4MAtS+9d8N7bmbUF4pv/nhGhkhqh5bKaGZDpUHtsCEtB8DDjf148x6VWbXTFGhPmz6WKffpzzv1vGzOhYY+g4lMzAdQjnPkcUXHorOMJd5/8Faz13b2o9WezveFaLXens6T7HEnXgwUxKDMqG0WQuW0aQ6DeJ5asYXluJtT5judJEC8M4ew2pAhcCsyOHPjQWWQJV4eGaVfQ7Q5ReNIRJEoSnnHtlW/b0lNw/eHhoAjf4A9k0ofZWHwO1+dSYk42jrH29YOKZtCiEcA3Mt7E0KIPwbwaf3nPIB97GWTUCX6ef24uP2y9ooMFAC+E8CPAHhGCEHC1L8IYD8ASCn/CMB9AN4rhIgB9AC860qde4hEObIeW10BsMISEtdSZZ8Eiq4C0M3uESWgY77QZaRuAiBB6rEvf+oZGoR4XG2P+yOonm8aR01fVo+U7XRWoU4tMXMR9DegvrxOEMBqtUwKS/t63a7qJ+hToGM5QWCOY0dR7piCZQ28HMaN6r10LKIcKa+s5DIgcnr0w4zXblU/YFrp6unw3vBzaNYuYMxxjGOhYbRDvo+TvZ5pDk+XSpi3ltFaPQKpnUdt75NoRBHu27kTD3yjZ5zKwqL6HO87csEElV+6cAEL5+9E7fEfHvgV2Mxy13H2R4C9/109MZzhJ6KwDniq9EWwz6ULb8YZtw0s3YlH57Tj6o0P0IDIyiCp38ozFBOB4dgxuH4G341e/PHsOSCjJKGVOGUJXNI3f1F5hTdAZSwkcMTEgXIOmx9P70PDeQthdlwJ9cMDAOGuGVJBcx6URRSZmgep4VGWENc2BrBi0KC/uepiqOZGUtdDZyg0mZkVlsxQKn2+bqejHqcpEEUm+3aCAPjSD2DdlDx/H9+sSQnIbWhmCyHGAUQ6SJQB3APg14UQezT4BwC+H8BJ/fghAH8phPgtqGb2QQCPSykTIURLCHEHVN/3RwH87pXe/xUZKKSUxzA4ReL7/B6utoho6R9uSaND9ABP6koACRKihdO7KTSUByvIsNYiiYCIBRO3kDKzL3ppxTLN4NSy4DDKDpEkgGVlzkQ7kbBSQWpZGDZoqlYOKgsoJ5/o1aoFqC88O660bQj9oxD6PWgYMDe0VwgS1DeJfT+3KqNeRlSt5lJ6ChY8qMT2dDZBy1a3QfW8QdcAqkxBtBx128ZpfVyatuYNTeoH/MnyMuDIzJHpKeQPPM3I5KI7UHvqKnS79XVbYZhlRk4vmwWhFb4uoThCYDYM0Zp7p9pOw4SpN5A2u8j0GtekYcwFoL4/hBJLPURt3dQvBgVu5PyLgYE7edqPGFq5LgcN5xVYks3fg96PvweQp5kHNKqplt+Hjr3ZNiD73Irnzt+HXjNIQc8uBCC6VvZZ0EKJAjVl4lQ2puctnSETknHrXMKbmxCAZVtX3vHKtgfAn+o+hQXgY1LKTwsh/lysszRmAAAgAElEQVQIcRSqfDQL4F8CgJTyWSHEx6CQojGAn9SlKwB4LzJ47GdxhUY28AoNFC+bpbbKJmj1wjjvlS40FHmdo9ZJ6rsaInU9eC1VGol9XwUWYuGk5iPpOIQj5kdJ1OPFBrGIIgjLgmXbpvRja6ddXllBc2oqB48l8aOiRGPiumaYD8iyBI5u8ptNk47Tc3QdievC63azLEMfN9YYdXO9usxGAQ/IT7DHmqTPNP3pHrCVYK+zV8lw6iBSt1Oj0Dfhuobb6XcXOqpGHI6YRrIjBE50uwpVFO4wOPvq8xP63K8uMBSNkzjqi9M3otCM7exH7xKAlTvzWgsDgkRqWSi6B3W/+sDkJ3Bwl1JbOzN3F26+Xk3G+5aFpzRvFlJPSYNyNT+q99Pz9P2lUmqRIp8P4VH5NBxR+xcdLD9usUzEsw++H6cRB7K/HfZehYCSO0bC7hudbzFAUFZShFtbbGHGjYKH/ihTVyK0KrnAQNk9QcxzfYyXYTjOsi+75t2SSSmfhkJ/Frf/yGVe82sAfm3A9uMAjlzN+7+6AgUsPWynS06dUQC6FJDU1A+ovJSf3pYqSPChu1zPgr6odmhe5zUzJ02ZBG8608q+V61m5SjN+xT7PsZOn95w5tK2IfRKh3/Biz2JQQGBauPUMKfj0XPFcpQdRQh1oBFJAi8IkGryQRPsksRkGv6ChkNW6wB2Ial29Y9a/7D9RlYq0YHiZK+HO2s1+ELgMU6CmFaA9cMo3/z/mHLUqZUbgbiG2q7T2FlZRnRKS6VexVzE5UzaSrGQWIORWNkKlwIF0UhQBkEOjqaF7SR7TJfi6kqoq0PG8LN4w63/CTXLwqMLOnPY9UUEUkl7fqmxK3sxR/lwfiye5fASjAiRi0zUW5PkTJlDZd9VdQ3aYRNx36C+AteY4Ggp/n6abdbcV3odOXkeZFIvy6boHCgo8sDFg0Mxo+Bmt1XwsDy96CPUVM0sarhWDJBl32aWSWfuW2Hn3aoJAVjWNx8ovtX26goUUijHGFFTUVdYk5rSTnbLsMKszGSFIaSd5qaiMXRWOQqnrWi2E0JntDVCI9xQ3ukOD5sZCQCGu4k3kmlWoj0xAScIcqgnKl+R5XoNyKNpEtcFGJ5c2jYCPYTHuanIuCJfLgCx6e7UshAPDysqdf1eJMgEwOhswOmp+rffUDxERMBHFNL1E0r/AYCszeC49XXcWath0nWNKI3rNRE5bfSe/TfA1EfU6+MasHo7zl68G7Xnd2z26b4kSzWCTH3uGhUTCaSd/fkSEdlmqm2JndGtk5OqzuVLR5U5wzI7vvMMABgq8kdaLSC+If8+tPKXzGmKMJ8hAMrB0nlSqYnQe7S/KFwHkAULO4TRg6D3AbJMgMSsyBjUlkSOAGh5UtdMrdfKLTSTJqKwjnLpEnqXblI7Om18+8Qcjnc6Sqddb0NrWjl6niXQOfBsiaOeOFV6AsDT94ZBXlNX5oM412u3uli/7joAMNl1denqpHAva0LAcbel9PQttVdZoEgNeZ+BxEI5Bpp3UMFhwMrQVxQT5osp9KosYT+u9WkgsRHU1ZHLKyvw1tfNQBtHHCVQX0xTFwdybLQc8kow1tw5aQdXRHlYaaocOx0nDE22wgMYwWY5rUd/aMhkGDx42FFk3ovMjiJAb6efQbxTO6RUrw6Z9gMANTjGHM6Y46CdJGjEsZn8NRPa/Md+7j5N9b795Gq0CEirK6yO39zoHIt1e3I0trdxm6udFZVsROZ4v9wOMeSkGckeke5ZFnp8pUxBipfwKEOwwnxw4EGCggqHzw4KbnYhcFDZkK/ci9KoepsoXVQ9idQzw3WuFRsYNCcQjOMY+6odLMf592prGg8xdMpsllRm4g1t+hyKZaZig5we88yETISao76c3056GKFafCSuC+n7SL5JqvfcW2N7Sk/fant1BQpLmOljO4qQhuTiQjObIJjjNQytEYBoj9oW1WAFQyrDKLOVByGp7AQiUk4+qlYVhFQ3NKnHwFfx3HlH1Sp2nDsHJwjM5Lfb6ZgMghw1d9hRtQoUZi548OFIqFz5TBshl4AsyKSMr0ratqE/5+dA+uCx72fEbE5bOSdvVf2jQOGtqqyiNpMFWr+h6Dc0xxBRPbteE87BP0Rv6U2ZRsXcNlIqILtPnb0eEFaUdkOFoYuIT6k9nTksGlwrOljowFhazVb55KypZESLCU2/EduX4FiZNnbv0k1ZHb4oI6qzVABZ7d0O88c1F8ZLNsj6EdJjgY0tcCiQVObUvrwXwY03uoEsODhZ1kkcXFxyFACOVio42espXXYWeE+tqfKh5PMd1F/gAZqyKp6ZDVKkNCWzWr4iyYOnw75HpMkhPbM9sT1YkWJy3jZ7rfR0DZoUZlXKB8oAZFBTrVQHAEl9MfsC0xeytApvUWpCstGsDg0AIoTTzr4UXISG9wJKhZU9ANNvGBRAzOELK2pbs7zy7YRaMpesnSIFJ8pUTDlNz07Q8QlOW8x0io+JqBBABuGszKlA0N2v/pFzWbpTqe6xCfchfx1nuxoabAdm8jdq34DIV2yo3orm3LI725JNtCd3KGqM4kSyDmy3Tn4VAPDM6pgKClw2dfnO7DtAGQM36WXAhpQFBqedbb/uIRUIRQavla2b87MTxfo715amXkJc2KfYYC6eF5CtsiV7ntOxDIKx8mOzITzENX0dwgwetnWQADKUWgxgptfL9NsZeGTclViKRC4oCHcNY46DpZVb8rTjCTaf++Dny+9fMasAssBI7ykKmVkKpH648X2+CXsto7gWTaamP8DRDkbzgT0GAKu1B6krVc16SEGVvYu74XU1wR4TI1KNMJHTjaDm2IYGM0FbWdMsAXLookGO0cD8kKfY4Kv/1PMQ+/4GHqmiNCS9lqa7+b6cNbU3qijGg3pdlcaqXP0sUYGBwyIjhly5pDmKRh9X8wjsx96KLTMUJlduxxr9sMeOAXM/BOf8LfDWr74EwIMekEGAu7c8mTWnyWEBalttBgdG5tGI9D2n5xfvzialOarJCrNBPI4s4tkABaCxY1kW5bQRhXVFfBeO6Rs8kR2/OMMAZM6MjDvuQY+v5OQGBQO6RruAWqL7Q2AEbaovIdCLyhC2ymbHHMdkEtSjmA9DFUg4zbm2Jc2DxuGzMpjA0qA5CrqXFDDpXvFrcVeBvtbm7uzN/bZMj4KuwVy/l5Wf6Lj8nLbDhHgto7gWTdo2rCCAw/iP3E7HzAjwmr1MEsByYYWBoTOm+n3iuogK09aEJOLMq04QINK62RSYOByTQ2elpnyAhs4W9+UBgT9HppqyYY6Wo9hv4BmMlabqX+F5KwwzGGyoRJ2oT0FEhyJJkJR14Zmv0Ak9092fd3Crt6tyjiZgI6bQfUNrOBc2zHDenkobC9hIlX4l6+5SiKHUlXA6EeKaVBP0ddU0NogrvuqkrCD1cHZ1EgdHFAXOst2BbN6tnBGHP1OlUoTZipcCJe9pELfSyON59BKhlmLWvyFINfUyOOKO9yRoGxl/zGv3g/bdbLqZHOMguCyQh6iy95JOG46VwHF7CLQ/JiJH6rkAaj4mkBKx3TE9DUB/9sGujQ55s8HBzcph/DWRZtVtHdg47Gi5+QY2vZ73lLgN4qf6Juy1jOIaM5HKbCoT2YofgFGcK5ZcvChCOCwMBLSyqqRNaTVOFlWrgG468xkEQ9LHmENpwKvYNN8Mw03ZR8r+5v0KOi7BVTnNOPFJhZVKrilOQRHI9zRoBV7U0UgKwSkpa5r2EvJNz/a0cp7rh4Eq06XQ8Fix42t0FXD9RZy7pGvX2vEuvHgf/BduhBVuTWWsffOSCj56xfq2qefx2WYXuPC9SDl+n1a1jC30QE1pRrRC9XmdWdXMBh2t6zDyeObQq3PKEdHqkxPJEaqIgorTzgJCAa0jRAS5dnTjcF7qwaxw6Xyp57BZgCjaZgFh0GR0cV8+vMaH5IrlHQB7PCCWqnEd6NITDU9y1l9i9W0mCdpJgiVNZUGSqBuOzbMicuL+qspSk1o+UNshgFo+CDvtDVr0AGDZNtIyo2DnA6G1mSww1E+oBQ19xttgQuA11NO1ZkKvoGlaNlee0asQi9XsAYUEqix2zbwC8TERnQX1OtxOx2QTwnXz76sdPW8sS9tGcaKa01DzFVHqeQALLHweomgEg+WWWhYqq6uGDoSfQ+z75hqKMxf03ma2QgcbALB7gLRTpFEtc5pxDVZnFG5nCn0OWV8/rKCu4YipaRtnAaimtT5G5Vx5y0Gi/M5fxZAQ+PC+fZjXzuETa7F6v9qMcvLkHPwG9u3+Go6UywaVMx8pavB5vc9Cqhz9vp3nsBzHao5j5xMAANm5McuUgolMhnTnCQXpXb0tX8IB8pxHALB2VM0WmNkGZE57UG9gq+Uk/hqyzYLGZsYzCr5a9xtA6hmuJwBoRNJIpFK5yRECE66bo5d3mGiTcjRsZV1sRvPtfH4l1ugtPvtBzW2blbR6Eyg9+3YMmqeWtp1JwwJZ/wlQ24mmhWZPSqsbjvFSTU1mv5ZRXFMmNDyWhH/IcVMTW1CPQDthmmfgTjmBXqXr5jA1rEM9Z5C4rpFN5aIq3LmLJDFMrRvOkWUL9DeVfcj4+fD9KRjxFRVx3JCmBO/L8GPS9VKg4NTjvBzH35f6M0SF4q+0EFUT9EdTwGakddUZVW6wQkTrh9Q2IquLa3AWDqLUWjXH3aotnf9u/NStT+Hnz5838Novn/7erMTEUFauv4g7qnU1r0Cv75cw5AWY8jxMuC5uq6gg6Fvquj596RJ6PT3cl3rKedVmsHPkJNa6Y2Z7tHpbps8BGOdqnB1Hf5HwEDlIrkQHDKa6GNTEvZIV5w74awcFnsTLqG14yUmDEpySQrb1Elv3DJqY9DyTPXCpU66ZTXMjvmWhrOdMYquLWErIQb0VCpp8PoL+8X2DCdiz3zMQ9FE0RQJYQir1gqY6k2WB0YihgjHvkWxfRgEIWNZrGcU1Z36zaVTbyFHSl40kRmk1TU3hBFkjmZyu0I3jlJV9AOSG44i+g88i8GMMsiI30GbGAwTvcxR/OJamK6DjknPnPYgSQzJR1mF6L3q+JLZtE1ABGMis27EgEq1x4XlIdp1WpRutrqZuSk0pifnrMG469YBv/BBKKxacoHVVAcLcg92fx+8++gFg4nM422d1ZU3OCL+BcS3TGksLH18OgfYtmSP0VjHlKcnUO6pVo3PRiGOcDoLc6lgdRDmStRD5jIB6DEVeouJMQFTIIugx/39Qj+FqbFAQGfR+RaMgwbMbmqh22lnAhKLjrllKvc/kGTRkp2cpANXgbmiNbZ9tb6cpgjRFjAiOo0XCZEcJHFkhhN3JMs9B19OeBtYPb5lug2aOMPxM4Z5gI9JsUJbzzdhrGcW1Z0SOR1wvhgyMNaL5KrvUaimRIJ2BAAWVOFZOKq+smIBAz9OUNL2HWxiMKxrvYVzJcfJ9+MAc708Auk9CxITs+qg8VQw4RclUOgaVxejaKouLpvQWk9qfncBePKRgxVrtDgAQjmBt9Qjc+tPZKnv+PjjrJSQuchPqV2PVT/+yenDm+8FZbfvXLePNN30ej37j9VjqqGwHbhvuyHFM7/660cCYcBxMuFX4loVjWgcDyDSUxxwHY1qoqJ02cXb5BlXWKvYqijV/nWHpG81q/mzfzRz3VgLGoB5DcXp5K2Uo3tzliC0yvwFYIVwrNkFTybsqvWyfwWNrlmX2mWcZLd3TgJekoIfxpDRZiJRu7r4oBb4B9wNQQWK9DpFcOZuIfV9R9JRW86gnTi3C4clWmO8/fZMm8NocxTVn3PnxVbO0bSTQ9MOF+j4NqnHH7THKcFqhE8Kpz/oMKbKmMc8iyMnHvg/JJqi5Mtflzn2z4btSq4XEdbF0yy2GhoD6E6ll5Rxybg6i8D78mEQqKG0bnfFx008M6nWlpa2fBwC7q67VWqFzOwqANI5vQnfvfUarI65JxKMrsFp7cmy1L3VewvD0hCHi1Uk8eu7mvHOJaogu3oVTZQbnrcxhT00rF2pdDABGhxvIoJ7LcZxHMJE8KcFiiQcKyPojxdkE/pg7rc2ygMvZoAb15V7H9x1E50Hn4bRNs1eICDKpIoJCKgEw0qeEaGrqoEqZRVw47Ey/D0cINZBXyNAcIczsRS/Jb4/4rkVJ2LFjSGoTsL/x+g2LpaKpXqDO7FxdGiSQQDiigiHn0iK02nbZaxnFNWj6i0rZQ5Eug5w1J8mLfR+SNb4lY3zlZSYKJoOCUTF7IKdGSCtgaw6y+KOggMOH6qRtoz47m/EwWZbhj7q0bx92nDtn3jun/a3vQ2Lb8NbXzXmRul0xyzFT5sPDSD3FrJvsegFh4mUzBoQuST31I790GPEBJeuJzn4gGkHqquFF0++Ays5eqvVGR5GMvqjqzsUySmVOnQdbpS44bZTdHibdTKa1mSglPkLyACqQiOoLkM2jg0sVfCVKDo3e/3JZwqBgcjnbDCo6KMvg50DGJ52LLK+FeRDJqDMifn7eKpYiAPFQ/n02Od8IKhAo6ZjMHAalRVo29yIqvB6AcuZ1LU2jCRrDG/8BWFH9BSuoGmg0UAgccVlfb77HYaDNlB3StDo1urfBxGtcT9eeCZk1rm1kdfrcnADDYBPCye10BtJiuJ1OjqWVNK/jAaubyw3QkQ0qORE6qtjQHrSSouE5gt8CQMqG7/h1OLaNVE9282soaabYItOmOV99zhSU0tFnsxVZqQH09gMTnwNefI9SiQPUD7MyB+z+YjaEt/uLap/Ehh110b/+K2p7exqy6b3kzCKpdtX0dephaPIzaK1qNmW/oejJ+fCXbiTHsouZfl8J7wCAJY1ONLk2RwjVtB6kA0FGjneQhgK3q8kENnvdoO2DgtJmxgfgKFOiMgzPegahsjYTF7pCf0RabBuQDwjF17PHQkSQ/d3Zc+TI29NmUZKmh2GFpU0zC/6+OeON89QDajO4taLc4jMb975qew31dC2alKYURKUiIIPGFss5xIOUY2vVKCJy2ry+T06XM7+mngeZJAZRRUYDdHzlT6/hJSLKfkoMrVM8R45komBBK3R+XpXVVRPkOuPjhlOKXl9qtRBUq/DW1805UF+HaMbNjEhNKvK8yhywS0lH4vTPq4bt0pvyA06VOSD1cGD/Izi7rleFq7cr9ElpFcN3/IWibQAwNPUxpLO/vOWPlKy9XxG+ua//ecUrdO4+tJ78zWwHglNW5rLSSvmcCgCpgyEnRUvHplsrDmJp50ojs/0+gp1PKIqJ89+dXVtvf97RqpszOAAUm8T0/HY0rgdJjQLZ0B6d79DMxn6E38ikU4va1HSO/Nw3TDgj26+4nbIUXrZj52toye0OZFKFsDvwLctAmB0h0E4tOJVlM+9inLvTzrK3PZ9Deukw0Jk2Q6GA/l0Rq2/x/tOiQZ/LrfV1PLO8H8+sb7IQeIn2Wo/iWjMhTB2/mCVQ4CCyO0A1fB3GvwRkPQsaZNtABz4ASlpEJ3FxIXLo1AMgxzz+7LMAYKCqnL2VSkGx76upct1Xof34ZPXyketRWextCGKufk+/2TSUHc2pKQDAsGbYpXPlwcgElTWgv1PDFp/5VXWhVghF162p3Kv6h5nUsOeWD+FsgMyZ+A1g4nMYdyVuq1Zx27iSAP3gzBRqV5FNBPU64n1PYecN/xkAsDb7LlgLb1aZzk2/pairAUXvQGUGvZqWSRVHhtRMwITjmH7EyV5oGt7nVjMY7M7hWVWeqsxlTk82NtJsEN/VZhPG5DzJXA0l5k3UQeWoQXBXen6Qk6bHIsymj4sKdbSNyjGbQVaLj+nvojYFm1AXIlJIJt4spn11YKUsw7Vi+F5gBvnIAinN30RCGKVOVjqjRUp7WmWSblsNptLnTjoznGywounfazO5a3mmG6t7sFnG+FJsmzIKIYQP4O+hR1wBfEJK+YAQYgTAfwEwBaVw98+llGv6Nb8A4N1QqP5/JaX8vN7+RmQKd58B8NNXkpF+dQUKKY3DFUliVulSQz+tNDXlIyCjkeB6u0G9bgJNMUNwNXqKNHJppoF6HUVyPYsx1SYAhs6fR1CvI9KMrbRf7PuwNPqKtkXVKvxmMwd5zaGttI2d/IYJSonrojc6avaJqqquS+p9gCpPUU8DQI56PUc+WKkA0s2R/1nBkKE3EUkCu6MD7ps+gIX1fTnnNz7+FO4ZHsaJbhd3VKt44DM/BwCozV/a+sepp9IrX78Ja5f+b7Ux3IF0338HRh6HKF2EU1G0HHXbxlSphLptG8dzvNNHkDpwhMDfXBjLHFo4grWRx7NmJwAs3o01ck5WmDWud31RZUdxTZXeAFXr5qJDHEoL5JE2VqjQUPx5skFln62Wteg5yqJ4OckK88gsWlkPUosbdFyOGCoay6YkMdIW6cvpvrDXR6mDKFXBpcY+I0JWERIN0AGIpv2phFabUWVNYsLdeSJ7r5HHgbkfynpmlbmM4Xj9cHYvqH+1lTmVLZrAtnE99QHcLaVsCyFcAMeEEJ8F8L8C+Fsp5YeEED8P4OcBfEAIcRjAuwDcAqWZ/QUhxOu0HOofAngPgMegAsW9uIIc6qsrUAhh6vecDM8KQ8TDw4g1Mqio4sZ5lgDkGtSDegq0L2UOqX4N7zGQ46VeAu1bWV1FGATghIK0Py9PkUO2kGeaLfJBcf4padvojpAG9CWg9A0g9UAZPfwG+u5RwG7D6+ahwylUhmWGFD0vU4LTxqfTpW1nXFDRTvVjZKv5mm3jC+vruLNWw6eazasKEGT0+fSHhoDRR9TGypzqjazeDumtItLOoV09j3aSwGfTwkuRgCOSzAmR8x55PCvFLN4NfSPUcYkfSsu0gprb3AkmhVV7sYTDnfLVrl5TLxPJ4qp1g0pdItwYFIC8pCpd2yC+KCCjJN8MdsuDIP2jYEb6I0QPUuylUBOdHU9aQCwTVdyHLj3p35jPfj+tWA1RkkXEy6XPT+z+PABAXvyn6n1e91tGNAvtaRXgm0fzhId0bwdon79U2y4KD73ip5vl6n8SwPcBuEtv/1MAjwD4gN7+USllH8BZIcQMgNuFELMAhqWUX1bnJ/4MwDtxrQYKIcS9AH4HSufnT6SUHyo8L/TzbwfQBXC/lPKrVzpukckVUKvm8spKzskDWdOa9zMMFXdBNrE45UzvRdu5HgWgMghZyCgo6FS1w1VvHpm+Ch8EpGsIhofNuZBClw2YclRqWWoWhEpiVS3ANPxc1mx2WWOzfgK4dBjdcfV6pxMh9Tx46+u5605HO8D4F4Glu+EvEppMwWk743o4i+oK8/cBk5/I3ZvZfh/3DA/jkxdLqD38Mxvu3VbNTKGTw7nwvfBWqggrb1RqhPp9e71xLFsrOHVpB8arOrCmHhYWD6t74a1mK871w1ndnpP/WSHQ0ZlEb785hjF6jszMT7Dsgiaz8xex2cUN/ruod8FV4Pi+0hssuFTsUWzQo2bZBwrZEM9yihkNvY4mnXPHW81TcAxoXpNaXs1ycpTljhAYY1mGmr+I4AihJsX5PdC9C9LMwNgx9XmGI3mOp8W7Nzbvba2nslm/56WYACx7e1BPQggbwJMApgH8vpTyK0KI3VLKBQCQUi4IIUhPdy9UxkA2r7dF+nFx+2XtFRko9A35fQBvhbqQJ4QQD0kpn2O7vQ3AQf3vO6DSqe+4/JElgnodbqezgTgvHhrKQV2BTIGumFEAWUZgKMnBFOzYTIDN+hH0fqnnqcE8djxL72NHEVp79xoHyAME9ReoP9IfGsrRclB5iVOdUyOc/t5xmspTtyL1bHRv+jqwRgGjDXu9rt9TmHNNhxYQVD3Y63WFKgKUc+1PoHLeBnEz8dJd4lvZwF13v3qP1mGDUY/vSfG+uTl8+eH3Xv4j24I5QQC8+A5zzxNXZVxxuZY5rcoclpbvBKwQS03moEhgqbs/cyTNo8CQuj4+xW3q71zQiBuHcvJeAOPCGmjcaRaDQ9FpkYPmehg8cymelwiVJG1vIr+do57o/YtN5yK8mPbtjwy+/rim7mMxYBWvzWYcWIUeB/WGCDbrWxYc5GcugjTFJM076Z/l2XZo3ssdPp1pYNC97+7Pl9L8hloUhSNZP4Ouj4tYfdMmttqjGBNCHGd/PyilfJDvoMtGR4UQdQCfFEIcuewbbzR5me2XtVdkoABwO4AZKeWLACCE+ChUKsUDxfcB+DOdkj0mhKgLIfZQdB1kUljw1tdNrZ9mCAjZVJyrADYyugpWu08tKx8cdFDhWghUXiLKD0Ctgomc0JybRkYlrovyyooJCuT0rTA0kFUKdrVGI8+5pG3l4EEzYV3ch0+SS9tG+R/HIG11y7ojI7DSFroTNqrnVf8mqlYRWnuV4x3uGv4ma+HNpkfC51BEkiDZd0rVi9duzU7qwvdCHP3XOH6z0kj+3KUIf/j0HbjKwssGo4CJPQ+rDcQhVZlTCKxiGQTIHIPbzgJEd3+2+vYbigOIO00+G6FnCczfxVU7b94OKK/oE8+/ZrPsIX+xmeOVHhAyh04lHn81OwcKbnEt492ywqyOz8+BMp0iYokjo2gb/eOyo9QM38yK72XnAwScNny3hyBNMeF5uYDByQcBIBACNdvGsXYbvdYBc347/XW00zSb6iYrNty9VeyptNGIIsjgcEYCOPycYTneLhNbV7hbllLetpUdpZRNIcQjUL2Fi+T3hBB7AFA9bh4Al+qbBHBBb58csP2y9koNFHsBnGN/z2NjtjBon70AcoFCCPEeqMYNrNoelFqtTGyI+Js0AsrT9BuDpqN5L8I4xgE0HIM4mIqPaTaCI6yATIeaT0cnrJdBWcHQ+fOmbFWcuBa+j93PPGOCCs8oihKqlJG0JzRz6+oqRJKgNpfBdsPRDux1LZfqrpgfEaHG3DCvZd2feh7W0ht0RpRlUOnuL+LE4cOm3jzhuvj1276KDz75xg338GoscV3VbyFnwCmiy43sR8kU604AACAASURBVE+rV0K6AFnZgUM4gayPwMsSxdJLMTvgtfli/2HQCntQwCgGFNOQJkfnZdlEUtsYTEqr2fWT1jZdA782nu1sdp70PAUFfk2c+oIC0NU41+JMhrYegHLpUk4tj6g+6B+gsotmkqDX35EhrNw1AKo8FfFr0Z+lcNcUAku/R81ycc/wMB6+lKGhhpwUNW8VC8E2lp6wbaincQCRDhJlAPcA+HUADwH43wF8SP//3/RLHgLwl0KI34JqZh8E8LiUMhFCtIQQdwD4CoAfBfC7V3r/V2qg2Ep6tKUUSqdvDwJAafSQpKZwqsWEAFU2IkJAIOs38IDB4aJgQ3mDggGfa+CIIVOm0pxJHE0l9TGLgYpex1XnyLo6I+KIrPLKCrojI7lJ8sbRoxg6f14htfQ1J66LYN8agltPGNGg9b0LqJw5oPiSdqnXeytViETNnZQaw3A7S+baqKlusSE8/4UbIbXqGQXkd7/932LCdfGJNeDOmnIMMYAH/vSn4GBrlOJ0LTzzk7atmGqBrMRkharcMjSTd0ikkMYlWqlERKt+cpxco2CQbTb3sFlpaVC2cKU+BdeFjgqzDUWZT5qRiGv5IUfJrrN4/kVFPvrHZ0D4ORZZbYv34EqBwgqzXhjPbtiQous1EaQSgWacBRSBIJEK0myFb1n4+GobgIey0a1XWt0URM4hK28NeQFqlgu/pCoJ7cTCfBThzHpd3RsdXB0odNyhuvr9f+nyV7Qlu4qM4kq2B8Cf6rK8BeBjUspPCyG+DOBjQoh3A5gD8AMAIKV8VgjxMagqTAzgJ3XpCgDeiwwe+1lcoZENvHIDxWZp09XuM9BIBIirvdGkNl95c/0GMmpIm7kJ/TfNYPBsgD9XFEQSlpWjG+eNdH5cWBb8TgfQQ4J0vqllocScJr0PKfXx7GF4bg690VG09u5FraF+FFYYonamDGnfaY4bRofRnZpTTVlLkeGl1hD89XWUWi0T9Mw9K2Re/O/url1Ir1eLm+PdLmqWhZ/ZvdusFBtRhGB0CLXzWw8UIkkURYevmW8jAa+p5lpMbledUw1s0o2wmBMt1vDJYZLuAi+v0P+DVtlF2wyqWsw++LkMyiSKDd6icBAfnht93AR41dwulMAIYUYiTDyDodIZ5zjaDPVURFPx/6kncbXmNxQdimaLBdSMxJjjmIDAmXuDNEU7SQzkZ6pUwr6SwLxYQ81SLoykWB0dZPZ4lH1EUHgYGF6qGCoroUB8c1k9X7c9jDlObo7jm7ZtovCQUj4N4A0Dtq8A+O5NXvNrAH5twPbjAC7X39hgr9RA8QSAg0KIAwDOQ+GBf6iwz0MA3qf7F98B4NLl+hMAIC1hJpU5DNbQWujVNjlOGmDjUFoSGOIQVSAj08tpQdD76n25ehyhr2hb7PtIXNcw1pJRQ33l4EHUZ2cBqJW71+2CqD0MEokhnSgDSS0LcF1FEri0lGvYt2//O6B5FLXn1bbySgRpDyFxV5G46h74TR1YqMw2ABZcvI/StpHe9O8N1cJ8GOK2ahWNKMIXtADUfBgChz4EnH/35T6yDZYc/hMzw5CmHsLajII9UuN81xcxXm6B1pnGsVE9vTiTwB0xH9IiZ14cLKOgwnmSuGYCf096XISF8l4AZQ2boYh4SavcyJrJjXuzwDb8XKYsyANZOKKCSIKNoj/FOQoKmIPoOYozE3QNIswHoCsZg53KpIpy6VK+aS2EUcnjNmbbqGvKckARDU6XSjhaLpuFx/FuFyd7PVOqIn2SMT1IyWnOG1GEZpJgwomxHAfwrRIA1Uif6fdxqlW+8rVs0QS2p/T0rbZXZKCQUsZCiPcB+DyUv/2POpX6Cf38H0ENirwdwAwUPPb/uOJxRX6Oga/GCZWUa0YzSm5eNhJJYuCtvMTDZyJoG8FpE9fNNCC0gy9mGdD7cBbZ2PexfOgQOhMjZkCwMz4Or9uFEwTw1teNngTPQuhcwrpCMTWnpjB65kxuvqL2+Hfpvxlsl/Fb0bnye3ElDYDU89C9+RmgP4LxUTXIR1rKj7RaGSVGGL6kpqFbfxqR1p4Yv+5RLHVGNaxRrY53+uuYcD0sUdPWvEcNQDtftiEnJ8J8c7coLARkDt1u5x1nbSZzusUAUXzM5ygGzT0Ujfan0hK9TzHTWD+cHZf3EhIvey0v99D1FLOMYjObjGs28PPl086bZVVkvMyk9/dFAIfBYGMpTSGS2Htrto12miKO49wQXiwV1TkFlUO+Dwfqe0X/AFW6GnOcHKU5MQU7UKzAPINYjuOXliVtZttXevqW2isyUACAlPIzUMGAb/sj9lgC+MmrOaYVx2YVP0i4CFCOkRwyn+LOcSshI+CjVfwg4SLKOKhhzbWtgWwmg7b5zaZhUg10EPG6XVSXlrDj3DmD0tpx7lxuUpoa1xT8ao2GeQ8qNQ1fuKBq+voYl24cRqWh9Cc4lLaoDWEypYJgPfV6eMDt7Adw+AHFmzTzY1haymr+x0QLddvGGQ1jxdgx4IV3A7g6NTH56G9j53f9LABguuRj0mvhKesjJstYWz2C6etm8NbRBA+vsb4DSWpW53JT0WLH1yBbN+dhnRxdxB0nyWQOakYXyzuXs8vBZIuU14N6FJTV8NcRwip3vvoxDc3RY7cwCMj/59c2iLOKB9BwJOs7UDZSRFPx4MvYhMulS/AtO5dRkLWTxJAx+hRA0tQIS9VsG8txjAkdRACVObSTBHdUq7izVsNj+ns86bpoJkkuS6H3pCBCAIsn5g9n4lLbZK9lFNewWWGoaKTZlLEp3zAVN+jHfFsxWyCjxrXDegkx+/Jz0R86jtvpGCdPIkgUPCgwtScm4K2v5yhHAOQ4pRI+PBiG6IyP5zio7ChCZXExlwFVl5aQWtYGzey0Xjf64Pw6i/0Xum+x76O7rwcA+Knv+vc41nYRpClOH/hjyPP/zOzrVE4oZ0DUF+uHAe8SwuFhhHtfQO1UpqB2OfObTazFWbnhzloNeyptBL6ataw7DtqJ4m56604bD68ph3rz6HkEUmK23weqL6hr6+1TjLEki8kdptPOT+mmnmohUomJ7xsVylTFgFEYLMsZX+GTo6XtgwIO9VJIF5y20X0tZkKpl6GlilY8Fw59JfNWNwbMuKYyNZq4BlRS6q5uLGvxY9M5+g30EhsTbiaf6lsW6raNRhRhLRjGkL+ee7lvWSZ4NOMYY46Tc/5BmmLCdeFbFk50u6bxPVUq4cP79uFXFxbw6UuXzLGATIGPoLjfPvkcnrgw/YrkevpW26suUND8A5An6bMY6oicIYe/mnkJ/Xdxurvo4IFsCpxW6i47Fmd4pW1caY8CF81D8CAjbduoyhWzksR1EXmeCUDtiQn4zSZqjUbuevpDQ2jt3Wt4q+h8ee+GjLInGuijfVPLQvf1f4c3aI2JdlLG0XIZR8pl/PDoKHZf1Kv5YAILi0exUMuYS/0FF1aaAEgQ3vAgcOrfbPKJ5U3atiEhvO1Nv4LZMEQ7TQ2z6FoIwAox01+Hb1l4w5CqP8+HSqVNJtXMYRHEsz+iSlLFlbCN/MBdOJKtyHkQoGBShJsOKuPQsXkw4RPCgwbuqHxEeH+a/aCyGte75nQUxffi58Qb2Js10+lainKh9J58loNeXzzGoEwrmMCQk8JBtpAiR7QQ5v+mMlPAILO5EpR+3EwSJZAkJe6s1Uw/43ing/t1b++IXhhSWYqOQ+91Otg6sGKr9poexTVsBO0kB0s0FwST5c5w0LQ1RzXxDIOU2sjJ0wq81GrlUE0cLstRTzRfkTI0ExEKcqElCkBF7W0KgJwZd/iCAoKFw8OmWQ7ADMt1d+0y5ahSo2ECAAWxUqsFohknTW16fftgD0i9jHU1CHC0XEbdtvFYu40fvPkJAMBfPfudG1J6TqWyxwPyJOqDjYIVNMZpNgwx6Xmqvu2qrKbX2Qs4bUROG0CME3q4sm7bmPQ8rLVH8k6UHKvdzlYBgHKC0QggWRPbW1UTzlEtY2PlPYTN5hHIik3t4rZiFkHHpgBBx/cbqs5HAUqEGTdVkaGVzqcYLCjwcRukH13kqzL3K9StLVZaGoQqo+d4X8YKUbOsPPmfZSmFwWAUonwONVvtW7Nt+BrJZOYoLAtN3VvgwYPKU80kMVnCvTt24FPNpqIBIVlWHXRm+33MR5HZPlUqYa3Ig7UNZg2g97nW7FUXKIglFiyzoNITOW+OVhpE/jcI8UPbOVWHYEgngDWCdQDi5SjKZIqzGBRg3E5nQyM5tSyAl7fYHIjJHnSWQloSlGnQEF55ZcUoyvGGO2UygMo+2vvL8BelOW77Dc9gz9RDWAiBQL+VLwTqto35KMJdQ0P41bJCj/zVC2rwzfnKA+x+rJh7trB8GBU2tT7IomoV/dc9Biy8FePf9j4AwJjj4mSvh1jKbBqXavftaTV4pR1cu/YiZvr9jU6Tl1Z4bZ7mLYpDcFVNMd5nK3dXl6j4cN9mcNPi3zxQ2G0YbiW7rafDvey9yIIJdR4dVuKhILFZ4OFZTrG8xGG8g7KdYlkt9TIUmc2ykcuVbAr9k4XAw4Sbyc+OOQ5O9HoQ5XMYcxzU2e+KU40DKihMel5OspbQTTHyFB+HfB+/et11GHMcQ/744cVFOEKoBjgjifylPXvw4fQiTq1sX6B4TbjoGjQhZd4ZF5wysNHxk/HMghriRebYYh2fS4hygkByluEA/ijKTHij3Y4i0w8gs8IQUbVqZgsAoH/dMnY85+QyB95joOPlrqmgNcFnSABVfiNRoODNv53Vn1dvx8LyYcBbxYJuSE+4qflBxlLiYEmVfYbGvorW7D9HPJ6hlzs3HkPty28FANQe/X60X6/0xGpfuwlFk7aN/l2/iH8xvgOfuv6/4X59vYd8Hx9qNHKSmg3tDFpEy6Gdd5R6iGozcGsvGqcz4bo4266oUhR3xpvRUlBW4eimOJD1LLbSzObPFwOQ+Vv/L72MaqNY2ko8FSTKOijyCXNu3NEPar4Xz42yPsqWohqAARoVCQsaCQtAhLoqBhV+PoC6p7P346naDMqaeqXXGweWv1txcjltLOlrPVBfRE1DXsnRz4chHCFwpFzGtP6OUY+DshRqfM/0+5jyPBytVEyW8cMjI/jo2hr+5rl7cp/Lv7w0B6S7trmhvW00499S21Kg0Eyt/xuAG6SUvyKE2A9gQkq5jSrkL7/Jqxykod5FcVq62MgG8hkAfz1t4/KoNBnOLaxUcqJKPNjQa3hPxY4iRACa07uBWDlyZ8kFsAQiHQSAtNBL4RBdOj4FwXB4GOWVFUTVqlnZ94eGgNIy3EO/gSiuZLrFtRnlYIMJ0zid7Qdo66bibBjieqm+XtOlEp6Ka2oQTu+7p9JGC28151Wa+Tb9KI+6MuewejucXc/jQ3v3YlrfE187i2aSmJq0A4Vm2TD/AKip5ZHjqjwF4CyVniLNhTRI3Y3+p1IN15fmxx80yT2olERG20m0iBrDvKQ1yMnTyt9vbDx2cUaEBzBa7VNvQbB9i7Ta5CgTTd1NUFuANa9Z5kN/X23Jpj2N3gt64TH8XJbJOW2DkFqOL2DM93Gy18v1JpbjGI91OmaBcGethlhK1CwLvmWZQEElpwYrMdVsG4+0Wjh4w6dx5vl3ZYsEbxXu2D8iunjX1V3H5exVllH8AVRh+G4AvwJVUv5rAN/+Mp3XK8K4lgQ57GKPoviYD8sVaTeKcxmkXgfAQGMHBRU7imAniaEOb05NoT47i1Krhd1PNXPnEFWr8DUXFF3Dyrc58C7uzgWg9tQScP1fqh/mufsAANXzHUTVKrpTS3AWrwcAxPueQvnAn6NuO6iXEjhCfWUm3ATHSk/iaLmMkzpLmfQ8BGmKuufhdBCYH+u9w8M4ceCPcbRSMYNQnzw3DW942CCsirBcfv/i4T7gN1CzLJwOAlVCgvrBv3/3bnyh1cJHdPlszHEwaVl4JkQeDdQfAUqrilWUsgSa3ObUHYDapuVbc5QYY8eyEguv/xO0dlAgGNTY5aWpaEQRP1uhotzgg33k/Mlxk9MmqnDal5wsb2bz5znsFtBMqgOa94NsEFNurv+xBeqOyx2fttN9puPqz6jVPIoniGbDiBRdgG9ZaAXD+JJOkL+0GgBOGwd9C4d8H/fo786k52E+DHFIBxtAUdy/f/dufPBrh/IIrcW7Ea1vL0T21VZ6+g4p5bcJIZ4CACnlmhBiezs+/4OMHHoxIyAblBHwjIKv7Iv7OEEAiwUL3lSWtm0mv9PCPAUAkwVIncGY8hiwgR22Pjubm8XgVqQLkbaN2pkyUi9QJe2RL6snhp9TjmT4OVQa6hid8XGI234CB0olnF08BAAYGjmJVmzjrqFKjsWzpldtgZS4V/8oj+ieRN1xgDg26JL37dqFz62v476dO815Hdt5Bt0BwYGsvb+M8tH3qz964xCli6g7exFLaerXsZR4rNNR9CC7FA3/I60WYinRKLfwrpER1G1Fvf/BmYpyWu3pwcgi3gh22krL2dZKaoByYDT9XOQ9IgTSoIyk+Jgau1wDpLSaZWbF0pAV5ktMlNnwQT8+cFfMMgYJJJE0qDegHxQWmv2D+g4cLVXUxCj2RQYFiisNGQLZKp8yvfa0+XxazVV1/d6q4XpyhEArGMaZbogzQdfMURwpl9XAHTIKj9kwxJ21Gv71rc/htx89WpCg3cZhO2yfcNG32rYaKCJNRiUBw2S4kTr1GrHEdQ3aqGibBRAyDq8tbifUk2QKd/x9irBTeg0/J65iR8egTIBTdRAa6uI7H8eOR74HAMxcRhGmS2ih0qKL2tOv0+93C6JqVb9GX89Nv4MJ11W1YE2J0YotuFaMIE1xpFw2gSLQZG0xazQ6QmDSdTHpujhaLpuacLWb4omDN8GyBT6rM4il89+NyiYBu33AxsFv+7f41LSiJP/PKysYcybRiCI1J0GBFmqSdqpUMuimd+zYgcc6Hdy3cye+wILTwZF5nGn8E+XoWwwe6zeyXgAxkdodJXzDV5vUr6DsgZe0BvE/bUYtTtkEBSDarzgdDmS9Bw6PLZa+gCxA8IYxLzUVbdCUNrAx4EW1jeJHm/Ud6Jx4YOHnOWhIsXhvyIoT4qYUps+jP2LABj0691IDGH0cQ16AVuhjSav7+lWVhXIJXN+ycLLXUzQyg0pm9oAA+pLtVdSjAPDvAHwSwC4hxK8BuA/AL71sZ/UyG80FbIawGWQ8OBTpN/jzfK6hONldlClNWPZBryHCQm78mABgaVnVS/v2YeRhH4k+ldj30Z7cgR1nl3NDc5Rl8PKOo/sv7YkJhONremMbQZqi1R3Lwyyh6v7NJDGDTAByKmT0P03BLsexed6yBGaeXsH+19UxpZuPP3L4OP589XbUXsgHTwDADQ9izHFwrK3O4b6dOw2/z3wUZf0IXX8mjh9ANS99y8K8XjX+5sWLAIAfHxvDmYa6RtMHIJ6mghaDTKoboa7k2Gn1yZ1LMmDlzVf4pvmLbLDPTEqPZBkDzwhIs8EO8+UYEQIoDPjx8xnk9AYFC25Upuru38j1JArILxpCHESzTte9WV+Gb6MyXLGvAuSzpc1YfGnanIJIOAL09qNVP6Gy4EBlucfa63jHjh040evhkF6UOUIAQuBopYL2Hf8On330F/PXsJ32aio9SSn/QgjxJBRLoQDwTinlqZf1zF4m47DRq3lNUe+6GCysNIUVhmbmgPYDkM1X6PcOdG2+qDsB1zWNZF6Wkradm74mjYmdL7yQvyYA/vFm7r0JGRWMj6MzPr6BLyq1LFitPQCA9Ov/J9bKavJ3/Ma/AKAGmY5WKqhZFo6127hL04RPlUr48MWLuH9szJSCOJY9SFO1YgMwVq1g4vohfPWR8xiZUFPgv7N/Nw7d8x/xwfM/tYGh13rmF3D0f3kAE7r5+HrPx9FKBY+12yoQ0X3Ug1iTnmdoGOajCL4WtjkdBLhHo7c+d+mScvacqoPEfnT5ZMghLqAeJisxmslKju4hctoQO5+AXHxLnjOKKDbI0ZFeBJVl+Ardbecb51aoZjNIHpScOi/pUEZBg35WqEAFRWfK+yS8tzHIuJMeNNdRPAY1re0QsBgUtxjYgPw0Oz/WIONDiiQ3a4Umox0v9RX1y3pdSeoCgwNf4qmge/FutC7erWjmATiTn8FyHGO23zeLnGaSmKAxXSptvSz2EkwA//NnFEIIHs4XAfwVf05KubrxVa9cE1JugMYCmVPdrKTE/weyPkeR/4ia0cXBOlKzM81shnqi15OQUFStoj+aGh3q4QsXDFGgEVqigbtCA53mJMLhYcPxxOGzo2fOmHPdce7cBvRVd2QEUXUMsT+JJVoxTn0EgCo1TXme6Tv8p/kK3jTm40+Wl/GhvXvNPoGUmOn3ce/wMIb0efWkxOrFLsJ+grmvq0DWXOohPuptKMcBCvr7WKdj8O2BlPhnQztQdxw4YWiykhPdLhpRZJrbgBqs8zVEl2Pvj5TLuKPWxZ8vMzGjcASoNcyKutUdoxPAmaQNIeJcuQJeE4DA9P4v49R5LbhEmUjMZgr0MdDZr5z7INlRjqZKvSxjoe00xyHCzPESOgtQ+hu88V2bwU4nxdriHWobd6aykCEkBUd+uTkPO1TSpUXnbBUCG2U/QMYxaYdZRlOcZi++F82zOG24/iIbpFOsr28Z66K+Wy1eiFL8g7OpUlIEsmY4mQ6iay/+MB7W/aclDVbYU5/D8W43Iwp8/f+lXvO138C226sko3gSmc7qfgBr+nEdSiTjwMt6dv+DjWr7xYG64t+G4oPpMwyi/qDQUoTXUn+Br6SJubY9MQGUziLYH+p9xxH7vske6HiCZS08ewCAsB5h9XpVclE/znUgHEETU+Y9O69roHZqXOlGjD8FABh9rIXK6irWr7sO0M3sZP038MR1D8Gd+P9wyPfxzOIUAEAMncJMX319fm9RqS/ePzqKmmXhrqEhuL0Ugb4D555vwnEtDI+U0NZ61bd8zyS+7+TJgWinUquFpy5ejzfvUQKGU56Hi1JBYH3LAvTncWetho+uqbIZOfR2mqIdhoZdlPoZvhBwhMDb6hXEUnH+nOw1sNCtmfr+W65Tje8vrQeaRHDNOKxW6CtHFkxg2V7IEFIkoWoxh0503539+VU31ez7I1mWQCioYimJHChRc5BRn4NnD1qwaI0juOozynkWS0S8/s6JAovPkZkS5ICVdrF0VDx3s88mZSZ+vhpA4OjPibJJADnwAqAWDvNhiF+43oUjTgMAZsOncbzTwamn35u/JssDrnsIAOBaqpm9HGfflynPw1JP04rv/iJw8e5t7VG8KjIKKeUBABBC/BGAhzSjK4QQb4OS4vufwjabuibbDCU1aDVME9eAChhhpQJp22YiGlCOEFFkngOyeQav20Vo70epqZqz1aVzA5FNBIWVtm1I/XLnQ6gR6Rl0U39nG3j27Wp7Zz/aN7YxfKaBdeuN+hzOwY4iDF+4gO6Ien37gA5Cc+9C48DH8YM6AAVpHYGUOOT7WYnJcdDQaf5ttSqE/mHfcGQE8zOXEAYJanX1A3Z7KZYigepmCLSZ96G9++cAAB9qNPBLe/agrstJvEcx5Xk40e0qpBWUMznZ6xmSOCKOu61SwWwY4t7hYXO+ddvGcauLs20AfgNfWlSZxp7hBny/i0ZkGQ4prjmxdMmDIGJB0ljmTWfKIIillfd7Ui+/wu+PZBoRfLKaU2LobMPIeVLTeFCZhF5PpH1knGZEFBxhsY9RXPlvpYQ0aOCPtm8WTLxVCK2GWLNtOJoToUjtQcGDZ4iBlJjVCwJAlZPqto1bX/9HeOZrP5E5++oMfnB0CPcOD5ue1xdaLTjIemyup7LcqH5CBdftLD8JAccb0Ie7xmyrzexvl1L+BP0hpfysEOKDL9M5vYy2QSk1/6ydpxQHMj6nQUGBs7HyyW2ecZBWBKfjpuN53e4GCC4xyJI1p6YwfOFCTgKUJsCpSW2T8JLWnXDWgdhmVcPWAbXq9RuKBgMw8wXrdzwO/+l/as6rPTGBWqOByqpydl7Xx+ohtcpaOvc2/JV2Wt9/4AwO+T4mHAdHNSx2wnVx19AQ5qMIn242DZa9ZAmc+PsL2DVZw4E3K2f8aLeLg76FM69roPp8Bk+ke1dqdvHUrJJJb+/7RwDAF9bXEUhpAkU7TTHb72vGWHXP6raNKc9DzbYxH4ZmyOp0EKCZJHis01EMslAw3tsqFUw4IWp2GfMaanmqB9xczquswQqz4LDynZC8/0ANXuJkIudY5FMiUkFvdfP+QdEpU5MZgHRGshKN38iOPWB2orzj6+gRxccgvqjNHP6g8+HOvpjNsEa3cNcUWoyMD/wVaUD0/ePEfMTrRP9Db8t9DlA05PQ6o1vB4NoTt/0HM7F9W6Xy/7P35nFyXeWZ8HPuVre27upNakmtpoXattyWQzuWHSeYYIJJDHESZ8J8P5JAVodxZuzIg2FY82UBsrH6C99ASJghDMk4gSQOOCxBAQMmNrbAGiy3ZNTIbaklldTd1dVd2627nfnjnPfcc29XSzJuGwvz/n76qfvW3epW1/ued3meB7vcEbTuOYUPveoiAOJvYa7bFZNPQaDGuqulOqzNd+ILh16GjbKNkkJljG0H8DEAoxDFig9zzu9kjP0+gN8ClFbXW7QF/ZsB/CZEMfB3OOefl9uvRCKF+hkAe6Vsw7p2voFikTH2NgAfh/C2rwaR9Vxgpjv99TKClEmFOF3Ah9DaBJoD5NSSDBJxDypyFkXqYevgvDV9B+kE6bzDhw+DmyYWd+1C//Hj6rUsFxQgMBelahX1iwcS51EUJRJnYQDOqonQ3QlAZDDhyCngxCvh7RCNQ688A+RqaNP0CwRiunjCQ+uHDmBk+2cVjcI/nd6M3x6LMV0oqBU6IFZ2JcNAfn8Dn58VpZzpH9+KykgeccxTpaIjZ3YBq1Pg5kpqAEC9J7kqtBjDZczBQdvGA62WWs5msAAAIABJREFUKicBwHShgMUwVPcQco7rymV8bnUVluSeAoAx1xVNTd9X72G6UMDBTgcTuZyirgaAn6nk0IxjTOZyal+LBfjq0uYEvKYztxJBXrY5rDlEcXMamaCdyTKAtShs+qdjOQDkcyvoRGbvZrTcp7OylgoFQBJg9OwlO1mkn7fXOCzhJzIgQx4V15yH2cs9byPJEiS3mJRA1UetgWQMOytPmtWxsBgTXGNSkIgWKdu/7eHi6QI+//JNuOWJJ9SxriGAeXeOjeGQXDgMWxa8OMbnBvYDAP5T7yf4pG2DehQhgDs4599kjJUBfIMx9gX52vs45+/Wd2aMTUEog14GYCuAfYyxi6Vu9gcBvBbAAxCB4gacQzf7fAPFLwL4PYgRWQD4itz2fW9ZhTcAKeJAfRtNPOkYCDrHmgAErJls0o/T8RcRkoChn5eOIXQ3mXuGw6vIO+QO0DcD378Wfl8/SvMr6tjc0RI6QywZx41KQCgnaqTz6F5zH7qH3wS0xrFw+kdgD4vVfZg7jQ+eHIAX1/D6UeE0Q85xueuiwzmOD7oYv0R8QXwvQqnfwcJVffgryWZbDQJg8UYYAUv1a9ovep+YbikcU9fad/HlWGFIlZwAwfmzGIapFWYI4ECngzHbRsk0FRq3HkWYzOVQMgyFBbm7Xlfss3T/gMBmHPa8lN7BZC6HqwabGLYsfLZeVav8S8fvx2HPE+JH2irbNkJBeUKjt0C6Ju9o2Ye+8nYyK38dBS4db0fOQxPYrKOXt7I9CeYnQYlez9J/qM/fSdfns41m+d7W3B9ZDw4rHhUBw4dthKkgYAFryknQtimmWMbgcY6Sto10KVIYHgiWrGoYYjEMsU9O95XKBg4ePAlP0o8DwK0jI7ihvx8nDi2jafv4zj8eBQDcP99CZcTFxKuft/bZfJfG2MbgKKTM8yn5c4MxdgjAtrMc8nMA7uKcdwE8zhibBXA1Y2wOQB/n/H55fx8DcBM2IlDI6aa957Pvs916ZRG6rQeoezLn1x16L/0LfV8949AzHZ2TibAV+r1z00R7cDAlmwpAkfzR1JPf3gx/1Ac2fRHW4y9S+7aLRUS2jfKJE1jpl1920jmoTycTPKtTwPjfqlJVsPhj4jLD/46gPY7/OV/D9X0iUB32PGBgANsbQKnfwdFHZfkqZ8Et2LhnZUWVFE6pRasPw/cTwsOwBGz6IuBWFQMoEQ3Wo0g0qOUzKxkGmnEs8BTy2XhxrEZ0dRrqimmiZBiYdF1VqyYOoKY2LglAIdCrQaCCxZzvKzBh2YrR0BziZC6HI5GmnNecRFA4JoB7WIfKu9dIqwZQY7nToh9BI6OAQIvL/zm30QlkE5YyHD37oNFZW/Im0e/UhNepOXT+p6zsKQUyPUBkS0n6e8sC64wk00uZdPz01C3GEMr9dO0JKimFnK8JECSfSubKsWzC8wBQjLKdIK/Q2r82NISlJxo4eXQVpf4cXvrrYnDjsa9WcWa+mfpb2Ag7z4ximDG2X/v9w5zzD/fakTE2AeAKAF8H8EIAtzLGfgXAfoisYxkiiDygHTYvtwXy5+z2s9r5kgJ+CT0K/Jzznzif458tRprZvVbmuumjsCnKbjpPr5HOOEaYoffQLcsLBSTsrVnTmWlXpfBQVnvC8H0UFxbWjMc25eqeaMLLJ04gXCoA2IWVHRwrm4RT73/0hMJYVB4Rf8idoQl0yYHpUpveaKKqNvo5AEBw9GaReXij+GUhLoeLRr+lSgAvm49RGRZfuPpiBz/2iufhg/dawBO/RG8ATt1G6Drwdnw1kcl0anjRQIBdrotrSwLfcdjzlDMPOVfiqc0oUg6datIEviOnQeUkXR/Z0z5PWsEe9jyFJCcWUjeKlCNrxjEOdSJYrCsCVE409Q91bIzYHMzswi1KTYwgD/iDSZCgLIHKNTqCmcpA1IuQvQtOY7Va6YeTI86yxeojullEtlPDrrdfgcNvkMy97fHeWhSACBY6iy412XuVx7INby1DooBmWWEqMyDuL49z1ZPQPwcAa7K7ehQpsj/lrPRGt9xEQSaU+uz6pJRlWQh5Bw1fBNbbjx/Hjf39ePWLhxC4Do4fEFV0w2TY8QvjuKu2cVP/T4LCY5Fzvufc52MlCJ692znnq4yxDwJ4O4R/fjuA9wD4DYiBq6zxs2w/q51v6en12s8ugF9AkgFeMEY04zTW2ovcTzc9s8gGCzpOd/oExGPaCj+LxibjppnCMBD5H6nf0dgoBQO9F6ELGBHKnO6xuLAAu9VS+3iVigoamx+eVSO0dquu7oHKPuUTJ5Br9MEvFOANybn06duBo68VDmjsk8BjrxPbhx6EceTXEW/+unIaRwwfd7HHcE2xCFziYiIn6sSLYYivLp4BTt4Cs0N/chb8ShsY/TTKW76isoQb+/uxO1/CKwcG8AJHvIcvd1qY933c22jAlcSAdN7pfB6z3a7qUVAw0OlGyCqmiTnfF/cH4L5mE6OSB4gcDO23KHsWOuAub0Z4RFb5ypb4PF0mVq9jTiLgNOB4sHKnsNApp5vGvYSNmI+p9xQxs7eUcDABImDoZIAA4NSwo9TGvF9PkxtmG8X0fyBQ54fvWMKud8mgextPxnNNzcnrwUcvi2XJDvWMQi8zxY5oZkdF8FjcN+mB0GQTZWfE8JrSmABS2R99drtcF/vbbXha9kDBPdvT0DNJ6i2VDAMVy8L15bLC23y8VsPd9Tr2NRoYs21cPyr+Tm8ZGcHBTgfvqD45Hfez2gY1swGAMWZDBIm/4Zz/IwBwzk9rr/8lgHvkr/MAtmuHjwE4KbeP9dh+Vjvf0tM3Mpu+xhj78vkc+2SNMfYuAD8DwAfwHQC/zjmv99hvDoLFNgIQnk80BtLYB7L1ylHZBnbWdHS2PoVEYkLk4LPHU1BJ3Yth4MQNBuCewOBXLxVYBgCDR4+iWy6roAAI51+qVtWxuj42/axnS6S61xkaSgklEYUJBRXDMNAeHBTnnfyAuK+Fa2FP/ndFn4ErxZqh0R7G0I5PKMEYQHzBK6apVhDkkN928iSqQYCRF/wBFh6TLUJZYnr5xLexv8UwLDOCN42O4pKmgYFCQZWIiE66JB04ZQ9E3zHhOKoX4XGOCdtWyHByLiUZJMbkOC0g0OVz3S6acYxrSyXsl8+O6EfIGQHAmMxcQiNE4FfQ8KQTL51EyTBwvDGALSXhYCdzOexvtzGSF3XyhY5Ah6uMwmoCyzIQcwcAl0C4kmCQBRKHncEaPF4fTbIHMuo5OLWkxKSP2/qDIkCQ5TLn9QcFEpqym2zfIVti0rML7WdOmZI+Dmz4cvQVagjB4xyQTWp9MCEElKOnrO9gp4OmzCpcbeFGPQ69RGXJwE4ZCH3ukzkxnECLiT2FAj5Ra2LZK+K44WN/WwSGjy4twWUMjYNvkVf5IJ6qMbANaWZLqYePADjEOX+vtn2L7F8AwM8DOCh//hSAv2WMvReimX0RgAc55xFjrMEYuwaidPUrAP78XNc/39KTnqcaAK6EGNN6OuwLAN7MOQ8ZY38K4M0A3rjOvi/hnC8+mZOvNwK7XrDoFSQIKa2D7LJqc3Qtykp0RlhS2NM1qGPHAeIIxvGXw249in7ptHQ2WDq+fOKEIvojhLa6V+3agAgiNFqr9zN0fXCFGHddgf0YaCT03MP3IWiPYRbzmMzl1Gqe5U7jxv4hHOh0sEc67gdaLUxLTEfFsnC3zGQIPb3LdbFAJabYwcjIw5j3bdwyMqK+8NOFAoKuj86qj2ok7pV6CW6mPGHJ65DMKZA4+YlcDvtbLVVvpmCmI7arQaDKHzpflL5iJUc2atuYMAzMdrsItFV2oz2McmERsJrqvuaDQNXVl72+pMxDfYSwlGQJMiuYer8NIEGYz9zeTGg69MYx9RCyLLb6fkC6TxCUMHWnuLeZ23Iio8gnDXm4Eq1OvFdZlLimOZJVqktdJyuHKpv6zYivyR70z4TMlY5/1LbVaxOOIwI00pNOa3AVsldlyfFaMhI80ienKqaZDBnEDgL5Ho7LiTDiH+tB9fjkbeOQ2S8E8BoAjzDGpCgM3gLgFxlj0xDloznIYS3O+aOMsb8HMAMRg/+LnHgCgN9GMh77WZyjkQ2cf+lJR2iHAB6HmM/dcOOc/6v26wMQBIQbdfKevQLdskEjK4VKmQOVe3o1vuk1wkQoZywdPp1Tn4TqlssY++wJGPEDKdoNCkq95Fepb6FTklOfguRNaxdfDGd1FblGA3arhaXLBB330KNn1EivTllueR78Kz+RYAZaO4H6NIKwhENuFTDEtXcUhHDMrZs2qT7ANaUSXjUwgA8sLKAehtgjM4pqECjOqLHLvgYA+OTyMgBTCc7QRErrVAduwUKrYGCiK57jvAxuo/k8LMZwr5xomQ8CuFGE+SBQ1CKA0Bs47HmiBCGzEqL9UOhuaRW52h2TDgkQwYQEmMbkZ7QYhmq+v+HUkkBq+GhGp8HMFhaWBdttve+wusaOUhtzXTEiyrubE6pyiXEgB77GuCN6QsTgSib7GcxsgZOTrk+LnoSOniYQICCD0mZ1v4qEkIK2HmCCEuBPJddaj6YcWItgpn6GFjwCmV0E2jhunScIbOoluFomMa+NMM91u2oQQe9feAAgg4N6NFofhBYVrsxCq9rfyE2VCuBL4seglPB2tcaB5auVzvxGBIqNQmZzzu9D7/7CZ85yzDsBvLPH9v0Adj+Z659voLiUc55ibmOM5Z7Mhb5L+w0Af7fOaxzAvzLGOIC/OMuEwGshZoZh5YWTXK+JfbbMQjeaQlpvOorO76yuisa0BMiRvCg0dTly6HarpSakuKa7vTo+jvzSUipQ6H2F0HVVUMkvLcGrVFS5CQBGDxxIjez2f0ewyrZGRhSPFBk3TSEWNP9KcHIiVjOZve+MKiczPXQK9SjCXbWaWrW/f/t2BMs+/nTTFnyiuSKI+ADctbysiAJp3xv7+3FduQzXMLDbdXFJU9xH34j4swqQrEK9OMaoZeHeZhPVIEjVn0l2VW9qWoyhIieiqAw21+2iZJrw4hh16TCorzApacr1FesNfX3Y324r50LB8NpSCXfX60n3LyyBL1+VSKQCCGp7EDg1DPTNqdUsAKCwiGWnBixcq5z/zBtqmHpXotNBJgKI2D5D84ZdqUOxOgVen06t8qfu5JjZO5hkDrcHmHpPsed5Z97opBva3UGZ0ai/BPl/EQDHzO3aVB2XI7Q6z5RuTk1hJ3h3c5JhaCUpyxJZXzOKoGrKElk9bFnwOFcguIOdjqJiUQGevj8SewEg1fMIOYcrn3nJMABZHn3bFtGn+ZNqFSidEnxZXC+fDaLwRD8EU9EG2fcJ1xM7ByBP7MTYNznnP3yubed9Ucb2oXfp6q2c83+W+7wVwB4A/6EXapAxtpVzfpIxtgmiXHUb5/wrZ7uuO3Ax337dnQDWjpoCawOFLnJE26kURFQdZxulJTS2juDWTS9rZTMGOq9XqSgktl66IgLAwpkzaEvRHhp37cV2G7puSuGOrqEjxoNiEe1tEbD1UxgYFqNMJYl0JrCaKv9AlAUmczn1Bb2mWMQ1xSKuQA73cw9vO3FCPDPGlMOlfcdsG03ZfHz95s3KEf9osYjVWhcrZUMFhJBzvOPUKezO5+Fxrspfo5Iy5LDnqfua7XbV6GTJMFSgcBlDPYoQxMnaiLFAMc+62oqVaMpdw1AjqMxsYSKXU+ObC125TvJGxcp8dSpxOE4NI/1PYKGxJY2NiEWWMPWuAczsTZzH1J0cM29Y7hkwdJt5Y8Lfpe87s5eJpvj7107QPR02s5eJ96QFR9V/6SVWlG20ZyjsAcHDpLRQNLMYw27XFX97Gq39sGWlMghqWhOyu6J9jwmIR+eumCbuWVnBZxcNESzUxZrAiZ9F35wo+67+4dg3zrf3uZ5dued5/P6H3nLO/XLGLU/5Wk+nnYs9dhRixjbPGLsCSerTB6Dw3V6Uc35WnijG2K8CuBHAS9eDlnPOT8r/zzDG/gnA1RBAwPOyc5WggPUDCK3Y18s+9OOovJPtdVBvga6d1dCm33ONhuKBIhAelYjKJ06kykwpPIV2LyyK0BoZgWvbimacRRFqu3YhdrroOyZWUO1RExj+MtA3I2rrAHZVhJD9oeURwKnBcoSTJgwDlWgAUZ5ZDEMsF3MYjWxV7hmTNWeaOgJEY3MxDAHLwrtPn8YN/f0ARPnKMFhqumnO9zFdKGB/uy36EpnnrjdKqZxBpQ3F62TbqABYyMwkEM2HPmo5kcvh2lJJ0H3EclAgKmLYAmY9D7tcF/VINMQDKbc6MvQoFpYuEydwaljo5sDyxxNuJgB5u4NwcD+Al6VKTjO3B2saxjO3BwB3UvtN/elmsb0XaV1Ugt7jeDqNspcUm22WqwpIB4gsiaHcP0FuMxzvciDOp0Zshy0rYREmgkeZjWTpPWhyymVp+pXJfB7zvq8m6w5KbYq58goONTU6FasJlGexOjG5Yc+KoweG5AK0c5WefgrAr0GMUL1X296AaKRsuDHGboBoXr+Yc95eZ58iAEMiFIsAfhJCy/ucpjvxJxsgAKSoJtY7rtfvWSdO5+51rdgwoIsqWZ6Xykj0e9enn8gWd+2Cv+Mh8UtHJm7tHPy+cXXewaNHMXz4MPxCAfUfEdQGKM2qL3XZFSWqB1qR0F8AgKiEBinfAbBLR4XTlCu1MUnCt/zNGvLTFdV3+MCZM0r4iDKKkmGgSWOMlqUc+s1zc/jA+DjmOh3VoN7fbqusgSafANn8lKtFHRtRpWayvA4gnMxCkC4BUClqQlJ1ULCpR5HS/KYSyCNtHw81AcBIiTIFho8rNj+Bh09dhvzAI+KRL/woYDXBnRouHVhQ+z584krkh76BmXd+CVNvfUlyI/kqpv5Yn2Sk5vZaByO2pzMHEUw2LkjM3CGCY6/SVfqa+r0URfAA0qSDVKaymij3zQGAEBXyBwXWJNRGaalRbzUBU3xf6jLb03EXJcNITdcBYqHgBQFKEm9DzfCSYeBAu41JmQ1CnoeGGq7Y9igeboi/C2a2wLuZZv1TtOdEoOCc/zWAv2aM/QLn/B+eoXv6AIAcgC+IiTA8wDm/hTG2FcBfcc5fAdGZ+yf5ugXgbznnnzvXibnW+MqWmGibXuLpxRprxDF4phQFJI3rbGZA5z+XxCrhJFgUwZfCRnS9KHMf+jVOXleEufR8AEBUOSP6CYN/nZ5c+bbAPsRuA3FZpP1nSjuAXA19R1gSTKgv0R5HoymvQefpjKepH9yq4lmiFd+nFw1sKSzho5dO4Frbxq/J3onFGN5draZm4Xe5LizGMNvtYjEM8Tn5fne7QuOiGgS4TvZ0KqaJ6yV/U8i5oqAmxPZiGGIxQycOpDONYcvCFifdzLYg2GfnfR+TuZya85/O53F3t4tqEIjGJ4CDHVl3j4qY89tq9PerS0UcNheQH3gEnc6IeDYa+vrQ6UG8aJukiA9K6Jx62Rr21myQeKaMAgI1qlX2InsXM3fUEjCgjgGRfZJ1Awk135X2hQACNnSxJiDd39CyC51YUG9WZ5UU9cxSzyQ9WZoCkqY2DSNA3I0Y5R4YkDxhojS40BnAju3/jsdXZ87x5M7fOH8OBArG2Ks55x8HMMEYe132dX2ed6OMc94z75OlplfIn48CeMGTPTfRXp/Nafei2dC3kzNXq/9MYCCVOyCZWMqei34OXVet8M0gQHP7dpRlXV+nJScuJ2paA0JkyBs/jcq3cqhf+S2xMSgBjUlYJy5DuEWKFA3fJ/7Rl5JGIoeqQH0aq5c3k2BQOCb0pCOtzrxwrWhgVw5gx6bDeLwmsTr+IB5a9GEe+G943U3vACAQ1J8+ejU+UDiIF9sFhUh91cAA7q7XUQ9DNcH0udVVtVoHki/TgU4HBz0PewoFVY56Q3kYnw6acBnDqORwAqAQ2CXTxLR0DAc7HTUlQ4GIzm8xhj3FYorEkEpUnjZ7v6/REP2MsIBPnKE9B3oS3F3av4JDp67szfoqcQn75eeXH/0yOp0RTP3BC1SD+JnqK5DNvGFZ9BMyNOWp6Sv52U+9p4iZt4oJLf0+Z/ZeDTBfnEs3wxcBMxKfT9mK0ViUbcxexIIa+p90yhkLMGJzNONkVJlGX3ViDWpe61mGAvJBG6GWn+lELpcCVA5bFkZWOYIRW5VOZz0P1dDF9WXxXf/L832o57ALDpncw85VeqIlQy9O5AsuTOoZRa9GdK9SU6+gYsQxoAWE7PnUMbIvQUpytJ2ax62RERUYuGkq1TkWRXAypabsvYSuC/fYZpjBAoYeEP2E+sQEorF/RzhaVVKQiJ1kZZerCRF6QASDqCRm9fvlCqo+LfaleX9AyHzmROOyqpfP3CpQvQHRnv8X7zpwLQDgty6/H2++7DuoBhbsvIWF4yI41Rc6uGGsT+lXA2KFP9ujwQ+IbOMdW7eqVWHcFup61/f14W6NvpzKUV4cY1h+FiXTxHwQqHFXOkfIuShXaBM1oVTjI5I6cuhjto2Qc+G8NAcnztlW01Z0PcW1pI+bUrAoHFOr4obXl6zen+EAoSworWmaz2RY3FJ9kXfuzOzL0qhuncLDaqLT7VcZScNqwh7cnwwQNDNrwLCEkaLor1nMlpkCS+lR6BNMWWZZpVAHDYAHpFD59SgSwwpymAGAwtmEwxxFxhSA0wIwHIYpMsinahz8+z+j4Jz/hfxxH+f8a/prjLEXPm139TSZLoWqN5ez0qVnPYcEqq0bQAA1vkflJF3MSD8PAecAQTAfybFYPQvxKpUUDQcALF10EZx2G5W5OYSui+Wd4sscVc6IQMCdRBpS9hSUrnOXehZSO9puJl/gwrEk81iW0yD+oEARr0yhs/PDytFtzwc4eew6RMP3oTwmRrnrkXDgJdPEhxYW8Oqt4porIxZe9PUarr1qJ26SSn3Z6Ray6XwerxwYgMUYlg+J8dotlw2g5MeqNq1rEFDJioKYaxi4eXhYsL9K9C8gnEhT/q5TklMWQcECEJNTFdPEsq+vYcX+QWzBtZLr7TJNXDp0AocWEqI/u/ItQbFh+Li8z8NsVziKy/s8PHLGwcybjz/j5SaasqIANXNbTq3o15u2mvndQ+KH1amkXJaT2YhTE38vOpjQamJk4Ag82d8CgJAzlCyREdT7hBpd4FdgO3W4hoGKKZ469QwosE8QFglIYSgAKCJI3aix3YxjPNBqqdIggR9J5AoQwWPf6ipKpom6ZB8GBHhzzHHUPZwTrnweFgOp/tmFaueLo/hzANlR2F7bnuXGe1JxAOcHvgOSYGIGwdpJJS2D0M/ZaxrJq1RgxLEi8csvLalJKj3ToemmoFhUE0vbHnpIla6ao6OIhgRNMqKSZH71k9Vt7epk4qQxldSaSVNAB2a1x8U/5iN3UuhHd7ceU+R/5b45NB7+IwDAwkMc0aY2MHsrhn9YlJ4+UWuqEcnXbG2pZvbOwER7sh9DhYICsM33eCZku/N5bItNVGXpKs8YxmxbjK0GAW4eFvd26/HjuKlSSa3wryuX0YwizHa7SlsZEBnMvKTwIMdQDUN17KLnqeY5HVuPtIzCENNf23NiUooCUJOIB/1Bxcwa+BWF/H2k7sN2Vf0KFw0fxZHqD2Hm7WLdNfW7Yr01c1sOU3/+9E0tZYF94lpnH8edevul8idqXAME3JvZW0ooPwDVy9Cn4JpRBNBYcljASE68vwWriSC2EMRAM0res5JBNQy1+qcATjoTQIJ/8bSAQToou1wXXhyrQD5m26iYJma7XRVsKqaJiVxO/R3Q514xTdSjaEPZY58TzWzG2I8C+DEAI5keRR+wRpLhAjCWou/OYg3WPWodIJ7Ro/yUtW65rBw8meV5CIpF+IWCCiZLu54Pd6mBwaNH04GFNBiWltS1KJhYnoe+kydRqIk/7MiO0Rx9PqLBedFbAJBbMlSDPO5/QqjdkfU9BmPh5Wq8tlsuw2m3Yfg+3LooiXUrFwmgV/EYGt++BbklOUV0xd1gQ1+DxRgeP/aT4nyDDwKGj4HCIu5tmOoL919LQ6iMuIrtFUhWkM04VpNLgHAM+9tt5OeaqsdRO91BfpMQHhqzbTVi+6HxcXxoYUH0KGQ5iYBz5DB04FbIuXhdvv1mFKnsYrpQwEN18Xx3lGIcaRaQmgA3fBxvlfAfNwH7okiVJyzGcKDTEcGWSPp0BbrmJAKJozjseSLAaHofZE9nkHg6TAQeSWYIiEVHaRaeVB0EkIwGy1KmJ7E5qF8hpqAq38ZkTjzjed/HQsCwu2gr3i5AlCE9zhVgEgBKcixbpyMnzrF7G43U3xOxAldMUy1c6G+B6EKo9JRfCFAZKeLxeP1FzHdjz4UehRxZgAWgrG1fxUZSazyDpqOWn8wx2ckofbQ1a3oze71r2a0WLM8Dzf+6SzYqc3PimCitnEfXoeyjcOZMKtBRz8Ot17EysRVmbUyVr9x6HZbnobiwgNbICGJHNlaXlhC6g3Dr31HvjbigDN9HfWJCbGsFiJ0y8idG0RoZQff594sbDkvgne0InBq2jH0RAHBDXx9CuABcTDgOXjUgVqzeSggXFnJmQtmgqKYzX9aJXA6TuRye98NF8Kb4ikVFE3nGFJMokffVowg39vdj2LLUdFPFNLGnWBTMsLat6D4mczlUgwDzGrJ7wnFgMSa4qDwPsETQGLUcPJ5RdrONEFZuBZ9YzAOGgYtc8eznfR97CgV8SdeCkNgKlbHJoB0Uj2F0+CRC7mNZJnHnA7R7ttrMXpaergtLonGpCzW1x5OexakfTw62mmisTmBxQKg2uoYBhEU8vOwAKINJGvdqkNB9NLWSIxmt1mm/kmGgZCVujUB4rmGoAETobypHbZfftVU3xqHITw07PFV7Tkw9cc6/DODLjLGPcs6feIbu6Wk0nioxnYtmnF7T99W36aZnFzTJxEwTPI7XnIMCT2Tbiva77+RJpYQXatfqyMat4ftoD4o6sAVaAAAgAElEQVQvnF8oqHO49bra7lUqKCyswPB9pXlt+D4a27bB8jy49bqg6IAIVLlGAyvapJU+6kvCR9w00RoZQWtkBNj2L/jRSREU7v/2DcDxV4Jd/D6cWhX1dq/cUk74hr4+lf7fZ3Yx1/BxXbmMjzxPqIf98enTmPU8TLou9hQKOP6+xwAAO163CyHnWPj2Ch77pqBcOH7kq3jRGy/H/rZoJFMNmZhkPY1Z9JpiUVGEkygRAPzV4qLCcdAf/bzvY1QyzS77Lq4Sj0YI3MTCeV9aFs7lUKuASq6LiuunRHQAOYKbFezRJUcjmT20xvGI/J+awWfDKlwQRu+5M7qm7zLz1u+kMyeds0qWOI+TrrcOIqwcUJ8njcGuESnSmGPpd0D0AxZlSZG2W7IXoSO7J3I57CkUsJ1ZuF8uPA5yD9V6sIas8KnYc6KZrVlb0n9fBiRTaheacBGANeho/edewUKn8VjvNSDJIlgUpVhkKWjo56amtRkEcI4cSZ2LnDVlFMQB5RcKqoTVGRpSOIvV8XHl1C3PQ2wYqVJX7DiKEBBIRm0j2xZUz3Nzat9OX5+iNy8uLKj7Cvu6wKV/AAC4/1u/Js5zYif8nV/DLtdFqSiC0j0rnsoi7llZUSv/6UJBrfwfktff7bqYlNlD4/NVXP76KXXcvO/jTROjeOFW8R6bK5fCWeXYWxiE1W+gJcvlH11awmIYYkJrQO5vtzEnmWrnul3VC6FGJ6A5Fc4VMyliB/tbGkeR+PBwqCVZeK02FroF2FY7TQ9Bn7XhJ0MBRG0RlkTZjqRIqQxjNxUaeOaOFlCaxdQfPOlp7++5ifKTCA4zbzyNmb2jaYyIp/1uaoHUagKlWVyaN3GoEyX7Wk2U3VWM2TZ2uSJqE0XMJ5eX04FBjsHSZ9qUGQKhsvXFBJU39bHqahAI4sh8XpQOIbKSjW48P9ea2X8DQc53I4BbAPwqgIWn66aeNpORfT109XrN66z1ot2gSSh94NaU1B3Z4ygY6GJEoOPlH5VesuqWy+gMDal7cet1+IUC3HodRhyroAEAttTI0BlhHRmsYsdJIb6z2hx2q4VCrbZmDBd+P8z9f4goHwI7PgoA8AcfBCoHEHJDrdotQJV3DrTbeLXEfRzsdLCv0cBHl5bUNEpTEgQOWxb2XZ3DgVOCUn/W81CPIuxvt1WT8VUDA/A4RyUyhfqIHAqzJK5iT7GoCAgt2TwNgRQyO0QCwKPShAsRLFzG0JSiO/LBgNnLKc6gkpFD0w5Qj4zUWOaY4+Ch+ak0TqAzmnaMWTU55ier69JM0tu4gG3qTzcj3fQGZn5vJqEuNzKBInYw221jwJJcTf2nUTFNTObKCkgJQEngXlMqqUGIUdvGvtVVwR6cYYu1GFN/N4D4fCj7oJU9fXaHPQ8HOx3Vb6JMcaMd+3OhR0E2xDn/CGNsr1aOelqEi55eY2cNEvT/uUpSumBRVisCWCt4RNiILOBODyKRbcMfGkKpWk2xvRKVuLO6qgKCGQRKhIj6FYBw/H5fX0p3QqcFsTxPMdh2y2WVNdB7WN65UzHVEuAv7OsCUYRo58ewZdMB9SVaDg1scQQPE30Bqfa7p1DAwwtbcLAgnX+3i1cNDODVg4O4Rzr0upxMIrEjqgvPBwE6nREsAJgvCKkRKjGN2rYCVtH1buzvx77VVbWy3OW6OOx5qndAQWzCcTAPwIqilNbBYc/DpESYX1EW7+PhVlOp29F93dDfr4SQqK8CAF89tT2twaA+0LUIffGH4gMDB9LqdFYTM28kZ3th28wdreS9S2wJK35HZGkZUKIuPERTbfUoSo1OU8ZXkQSSgBiFvaZUSn3u1McY1qajABFA9hSLSqAKWJuN6Mp5FcOAlxm9fSr2nJh60oyWt6cYYz8NIZ03dpb9n52mff69ehVnIwkkxxsbhmKEzW4HeggUYe2EVWTbomkMIJLnocxgZft2BMWiKhVRMzp2HBUogmIR5RMnegay/NLSmjKXLtNKjW+avDJ8X+Ew9POH2x4VJygcA07+LPDEL+FU9QZg/G8BAOW+OZw68ePA8tWwd/0ZAFFi+sJjL8blz9+H33oeUDJFUBqTrKBzvq8E7iccB3PdLg52OrAYUxMp876PjhzpXa4IfZZZzOG6UgnVMISrIbP3FIu4q1ZDyDmulwHw3mYTu1xXEPrJHgQgVo+jto1qmOg40+TLYc8D57bi/LGtEDf2D+KT9XpKx4L4n041B3Gkl06D+mORK2dymFR+4Y741x5PAgVlF6VZKM2IC9j0nsvM7SKT4HIU2zZEACCnbiFRsqtqTMG6YyXCRgCKKobwMNf39amFwGHPU4SAJYm8BqCy1noUoaRlFCR9qwsi0Wt6ieup2nOima3ZOxhj/QDugMBP9AG4/Wm7q2fIzreZrfc1skR+ZOpPSwsK5KAtz1MaFoBY1VJGQat5y/NgAKrfoF8vsm14lYpy8npzvJcCn+H78GVGYHmeOi503ZTetlcoqIkoAFjdulU1vbsNWW8f+ySweC1g14DVS4DvvBYA0CCyN8JrQIymoj2OR45ej0ecGu6cFq/RF+Xuej0ZR83n1bjovkZDTT1NFwr4EgG85Ap0uTWOd/kP4jWbXOzO51VpIeQcrxwYwAOtlnI09TDEfBzjpkoF75YNc0BkMB7naEaR4hI60rYAWGu0rIOwhP+5WMNFrqUcDlGBLNd2Y/vIIRxflscUjilep5S0KLA2q6C+hV5qGnoQWLp6DQL6+8EEuG87Zm4XOiY0JhzIZr9thKnV/EQupwKHDrwbc5wUDsJlDM0oQlXfTxI7epwjjKI0ZsJxFNsxgFQgaEZR6u+pGUVqtHYj7DnVzOack2D3CoCXAABj7IIPFLqtJ2ZEr+lqdOuht7NlrV4ocP11MwhURkLTT0aP0TwzitYEEHFQIOjDJWqbSmLcNFV2oKvtFWq1lESqs7qK5uio6mcYcQy3XhfBhFS/Dr0JuSUD3fIlay7vnN4Mf1sTweouAMDC4rW46oc+iof2vw5X7Xkvbj8usoe3bdmC+5pNUWuW73N3Po95KZHaCfKYY+Iebh4eFqOmBhKHawn0+GzfLNDXh33yve0pFHBXrYZbN21SsqukpPehhQVUg0BlBAc7HXjSKaieChPlCDW1LwPFRaU2jtRHUbVO4siq5NzyxwHDx5bhGQAs0ZjQR0HJKCCYfjpYRE66PwGIIPG9ovN4BmxmLxN/S53RdOlJqt/RGCwggjz1jKg8SHiJ3XJhAWha51HCRuwyhlGZOXja4AJllbo2t04cCWh9rExZcSNso0pPjLHtAD4GoeMTA/gw5/xOKVP9dwAmIKRQ/x/O+bI85s0QSqQRgN/hnH9ebr8SiRTqZwDsXU/OgeyphM7XAXj/Uzj+e269WGKzQUB3vueyLIWHHjiyDLBZQSQqNemvA1BZiL5vZNsp7ITe+M7iNngUoVCrITYMdIaG4EtNa2qI04gsAGDkfjTtq4UTDKTjG3oQ3SEIMJ1bRd4U76HT2AF/3MGO4aN4fE4C7hqTeGj/64CxT6IaBHiTxH3sb7fxpVUPlxcs1Tjc325jzLax23VxaGEQjSWx758Y96V1DgCxAnermA8C/PJMiB0V4aTnfB/VIMA7Tp1SIDwC3JFzIOdiaQ1NKl01FQNpB5O5HBZDkRHMdgNcVDmD+YBjR58IQNP5Lv5puYWSYYhMRBffkStk0lAAAN7ZnhAwpj4QJz0ZxB1cgLRp521EgT6z10mX2+Rz44HE2phJv8HVSke783nFEEygymGpk14yDPW5U2Chz12XsD3Y6eCaYlHt60oqGPpZR5JXTHNjS0/ARnFHhQDu4Jx/kzFWBvANxtgXIGQg/o1z/ieMsTcBeBOANzLGpgC8CmJSdSuAfYyxi6Vu9gchVD8fgAgUN+AcutlPJVBc+Pp+0vSegt5LeDJBoie2AsLRK4nTDBYjC+SjzIPU6wDRN7A8DwuXXYZuRSKFnRo2fWMBXqWC9uCg0vj1KhW0R/oBtwqzvkm9B78SILckxmYpe1jctQuFM2fQHOsHtgq1WfM7/wFRRVCJu4ui1OLxn0gU3JwaOjrAqnoDHj8zo1bXW658G6pBgIpp4qbKUKrBfP32Mva32woA5xoGRiW3zm07l/Dn94tJ61OPTgs+oU5mEqg9juPzJSAYxOOx6F083q7iooKgOSfHsDufV32HyVxO8fuQJGm2Jm0xBjeOU45kdz4vJFJdF589IwLy43UHMHI4EjdhW23lyJqxBy9uIwgLGJWD4/UoQkcX6iGj7CIlSPT9GyRSVppNKQAqKVbV41nFKR8YsQWFOD3ffaurCoSpo+F35/O4r9lMeJok/YZSNiTK+EJBlZ3onJO5XEr8iGjrXcNALga89sbNKW1Uj4JzfgrAKflzgzF2CEJU7ucAXCd3+2sA90Lo+fwcgLs4510AjzPGZgFczRibA9DHOb8fABhjHwNwE57GQHFB/oXrJaBeMqaGBpDTg0SvQJCdYlqvfJW9jh4U9PMbSJrhRKvBTRPLO3fCDALk6oSBKKM1IspJseOojCCybZFkBiWVWbAoUjQe+n3EQ48irm+D4ecQn/xZcXzlDOCNwvRixI443vRiRMPHRLCo3gCUJclgdxT2D9+KkHPw0z8FADh1+LXA4IMYHv0Wri2VVL35gVZLNZNfJcGBDzSbSkCmYprpSZlYNn31Wn84Le4h0Oixc1UcOTkKDN+HsE9qeRcKsJBIrVKgoNLFhOMobMViGMKC5IeSs/YAVEmsERoKE8Nyp0WW4A8i8EZxSgYBlj8O3tkOlj+OU03ZjKb7JodI+IpI0mtHjlhhS8vyMH0/2cxtOdhb7wGI/wrARX111COOunEGQSgWPw1JwFiP2nAlvgUQAYAQ/LTwqAYB5nwfu10XB+XCh6RrafJJB9wB4u+BAgVpVwzkcmg3AoQtERi6EUejG8H3NjBQ4LwDxTBjbL/2+4c55x/utSNjbALAFQC+DmCzDCLgnJ+S0tCACCIPaIfNy22B/Dm7/ax2Lq6nBnoHBAZR37rgrFfzF+jN00TWa0JqPdNf10tP2e3Z64WuC8vzwDKU5CvbtydEhNo16J+zugpvWNIkN6VwkleGX5GgOyIIJD1jsshBe6QfuXoL3aIszywNIXaYKJXJ3SzPg/n4VQCugj96PGGlNX0ER28G2/GXqqG9ZeyLmMzlUDFdNSWk3p8EQdEX94b+foV9cA0DV0wLouKHv/YueX/6cy6JAGg1BYCNavw0n786JZZaAIatRaFRYRgoaXoUBzsdlEwTD7RaqXl6D6KERYhe/X5tI8TufnH8wy1boK290UTPAQBv7cRA3xyWvYF0gAhLacEf+iwAAbijYBc5yCrWfV+ZIcaUq04bc10BaDxy5gXYPnIIJc5RN9Ml15CnwZElM5HPJe4w1zDgyTFncmBE30Fa2mREUlgyE0W8immKhjXnsGwDzRVx/nbDRxxxhMHG4SieRDN78Xw0sxljJQD/AOB2zvkqW3+Ut9cL/Czbz2rnovAon+31C87k48g6aqLOoFU4Na6NOFZTTDq4Tj++F/4idUktSOgN8RhraUFIG5ubJiD31ak0CANB13TrdcSGgdJ8AuCjKS3qYcSGDWAnYseBXygkGA+3ATAf3XIZ1nLCK0UjtCmcyNA3hBPU6+vSEfITvyCEkSBWeqd8YIsjOHZIInVCS/Ur8jlWgwAVufKb7XbVeOzDbhVoZRY4FDQaOwAzAjrys7Cl+E1YUgFsvvQZsXKU56ZadCjLEbrYTYg0MaA+gUNjmhQ88qZgJ11ANQkCAOAPivq44Sv2WLTHBX6ABeCtncm+WXEj8Qnj+zlQTN3Jcf/tV6O85SviWQBA4RiOz79Q4ElWBSJfsRlbTXj2siopzXMuBhC0QE4Zg96g9uIYrtQRCTlX+iSUPeiLlJJpIvIjeK0QzZWuCgxeO0Sz3lWBYyOMY+MAd4wxGyJI/A3n/B/l5tOMsS0ym9gCgKiK50GweWFjELCGeaShDbT9rLZxc2AXiGUDBJnqU/g+IP/IyGnr/YVe47JkWZrxXtmFbpbnrQlK3DRhyHFaOo4oxbMN9+z16Hyh66ptseOo/Zx2Oymr+Tl5jfaaSSszCFQvIygWETcmE6rynJz26YyKn71R5aT51k+BDTyEkpHDfc1mChXtypIAMYuGAN6xdSsOdjq4ob8f98ippZdf8//hs/f+USaj0CwyoZLZMC9KUaSPAGD52E1YtprYMX4vKrmcCgJEQjjmOKok5jIGaDxCOhcQ8QtRCSQIC+gYfpLFqA+xKRygts0uCdr3ILbTcp+AOJ7q8wDg1DDzxibgjZ6zBDVze5Dpb2iv7WXPmhIWaV+wzZ+HxRim3vwyAC8V3E+AeK/vtwFclehkvKcIYDNm9jJwq4llqaOSz62g6XmYlaVLQIxZj2qlJEAEBBq3JuEpIF1yorHXblN8pl47hO9FqJ0Wc2+rNQ/NFR+7rhzZ0OexQVNPDMBHABzKKIt+CoIp40/k//+sbf9bxth7IZrZFwF4kHMeMcYajLFrIEpXv4LzkN54zgWK9foI5JhTvE6yX2BGkaL7pnNQppClKtczBdrP8H0w00ydg17Xy0mAmH6KbFtNJxlxrDIJsjXyqhqLLGUDlB0Zvg8DSbZA581pQWrNeT0v9Xy6Rj/grMDwyoh9IU8KZ2WtpGV7HLw9jiOjn8OA42FRHk+TRq8eGlKNw7vrddzXbOL6vj7UwxA3yuZ9M45Reenv4n//29vXDxa6hXmxgqdx1dY4kKvh8WYBLuukwHUhRNlCp3gg4NX+dlutWJsSkKWbbbVFycM4gyC21IQTDwbSBIAQQcW22mJbrPVaeiG4KWgw/5x9i6n32yk1OpJThek/q8gFk3v/yfR2DSsyc3uAqffbqfd56I/+FVh5gVh8LIvFR0cuTOzKt9RnQp8P/f0AUDK5lD2QUUlqwDTRXqUSk3hu9cUOmnUfzRWxeBl9XhmlfgdbdvZv1KNAzDeMEuSFAF4D4BHG2AG57S0QAeLvGWO/CeAYgP8IAJzzRxljfw9gBmJd9l/kxBMA/DaS8djP4hyNbOA5GCh6NaezTWkyAqtl6TmyE0xk2RU/ZQmUmehBKqtlAUBpaMeOk2JyzTUaggZEE1QJisVUwKJ9AaQyh+x71rMhQnzrwY7en94MB4DIzoGbEWDLLzZxGbFMmm41gcVrsaw5xEODD+JlIx3c12xit7xHfUTVYgyWvM7Nw8OCluOqvVh44ANrnnFPi8xkFNXwAc8BaldjMf9vyvkT+tvVarq7XBch5zjseT2Dgy6MQ1mHxRhghAhpV8OHbbUFdYGGqQjCwtq+UC+jDMX0gbA37UdKX9utIja2wIhjDX9xAZaucjXM3FFKBbhL30KBpZdQ0k/iiEYweMoQvbdPRqLSMuY4uL5cFhkj59illThdw0iB6HwvRBjEiCMOt2hheKtYPPUNurAHnLTk71O0jcJRcM7vw/qTpi9d55h3Anhnj+37Aex+Mtd/1gUKxtjvA/gtJKSDb+Gcf6bHfjcAuBNCQOmvOOd/ct7X6NFPyJaXADHeardaa/oTWecK9G6Gp+g8tPIOi0TTWQ9CQbGYIvLrSEK9yLbXCB+p/oPjpLINCgT6+zN8X/FFmUEASLyGmrzyfdjaF4NkW9cfE5Z/9P4gYMrmMoHzqF8gLpyUY1am8AXjAL5gJTQOu1wXN1UqOOx5mC4UVC+BN0OUGyGe2DmFofg/AwA6D/73Nc927cPWmsOmD5z+CSx4o0oKNuibwb2NBji38YtD4pntb7XwQKuF12/ejM+trKTI4QCAR0WEWrO1IzMcxoKEQDB2EPiJCp44QSl5/3qZirbHztpR0VCW0FTgTZy/DsgTfFAXJhsplZnAhHZFNgs6W/ls6k6eZFwUUIMSAvl8m2YDH6/V8LnVVSVwBYj+2PXlMva3WqoZbo0K5cOtLQ6vHapA8emVFcwtrmIjbSN7FN9Le9YFCmnv45y/e70XGWMmgP8fwMsgmjMPMcY+xTmfOZ+TZ0suZFneJmAteZ9ywNoY7XrnViv4ddT0DN9P0WvQ+arT0xg9cEBtj2wbseOoc9O2bFDgpgkmg4Ju+rgvvcd2uQxvE8Pg4SW1HzW7dY1u0r7gpgm71UqRDMZOWbyvvKbDoOkTqCmfWKzwASCQjrC5/d9xX7OJed/HgU5HfYmvL5cxVi7AjDiaV1wBAHD5byP4P3IdkKulVfrMSDgeuhaNz3J5TXldMB/c8IGR+3C3+S8AxMjlRC6ntCqoR0EjmwBSjLKpbeTo9aCgU4Ho2hR6uclqrs009H0o6OKpK96p+v+zoHcxs5clQTBfFUSIv+enFxZhCTNvFOXMbJkqhWbXqcvl6PFCW6gKVt0zmC4UcJMsZV5fLqtx6Ksc0dvitsRQVEycfDwJDIu5cA0p4VO35xCFx7PQrgYwyzk/CgCMsbsgACZnDxRsbRAA1upSmBlHm9XB7kUzrvoRGZxGr+vpwYYCReHMGdW0Hvz2t9f0JXplMNT74Frjm0pSFBCoN0E0JHSeQq2G4kL6fTrtNrxKJdUDMeIYvuuqrILuVzjobtIjAMQXWON+Sq2wASWVCkhWUFnOmQSU+lhT0nyM2jaachpldz6PhwcOiLo184HLf0+c74lfkvfiJz2KXFWQGEqb/sj/Sr3HA7/90/C2fBqAyBAWOg6YvQyLMXQC2SQnp2010xTh+vRSnMkiem3L/kzPIjv95A8qfQraXzlWzUFO3cmflLb20xkgzqd5PnNbLvlcdKPAmgmgdmFesQk33i2U75pRhEttG4eWtuHnt4lFTcU0lUYFlQYXWkPYXl7GYih4oGg0ezqfx5ht43k1jjNLyWCB5Zjwh13suGJYEVXCQ4oxeCPsucYe+0zbrYyxXwGwHwK2vpx5fRuA49rv8wB+pNeJGGOvhYCrw8oLLAqtkHtRg/dSssuKEdF+etDQ+w60zdTQ19TozhoJCRESO1vC6tU/YVGUCBxp+xoAQPegOXsyXVY1S6cOIBUMyXxJHOi02/ALhUSgKYgR2XkRROkWDR8IBgWBIP1O/0smWBqH7ACoFuYxZtuC34ewDZwrwBv1MQ52OsJJm/L8i0JaFP0zKG/dh8b8K5JglK8C/TOYfs8ja94/AEx/8F9w4D2i7m27ZxCEJfDYEYR1etMZSLIF2qaXjrIltrMFD9pOP0dOImZEeg1k+pQUZR/y9ZnbBF6GggiVpDZy4mnm9kBlNWcLSOd1PT3LAtLvzamBsSCFeaBRVgBqwmlYUnhcOnQCTfkciWbjTaOjKgsUeJmKksDdI4c2qkGA3fk8Qr+Dtpx2iiOOykgeXYdhzvNUBlENQyFetIGOfQOb2d9T+54ECsbYPghyq6y9FYKH5O0QwfjtAN4D4Deyp+hxbM9PV6IbPwwA7sDFnBx5SsBHZgzrge70clIWPKdvp3IQ7R8Ui2hs2wbD99F38qSQE5X7EgZCzy4sz1POeD3iQdqXHL0ZBElGIdHdsXYPgOyPyPenB78s5oJox2PHURNapWoV3DTFa3GcQoz7hQLCop2UAmLZH+COCAyEK2hOCueusc3ahXn82tAQdrkuFsNQOYYD7bZa0X3w8MXi+PbVSdO3O4iB8bsBiPrzh8YvwiXbj+INTUEud9fyMiY3P4GH7/hlYGUqXbIAxL2ufEq8X6mqBn9QKayp9+HU0iUkbzQtRKT3GGjiSXeKevDITjrZzbSID10zSyxIkqqUbZjpla6aeuJOzzJTz223ByKYxk5P/Yup99uYuYOygKc4SaVNdMH0k+m4WFCtcwCB3GZbbUUGaDGGkCbQZElQx0FQcKlHEYblz1S63FMopHQufjpXgtcIgUouuS3XgmEy2J0YFSeZkpr1PMxvsMrdD3oUT8E459efz36Msb8EcE+Pl9YDk5z9uoyJOj3WJ//TzZFCP2ejIddr9tmswW610HfsmJouorp/UCyiWy4jsm21jRxvtjylG2UR+spf348CgaXhMLLTT6rPUS7DrdfXlt2CAM2xflRmE5GkSL4Xuke6lhkECCMX6JPlJnJkhWOqYQlAOIgVkUmUNwlWAS8G7ms2hRwlY+qLTlTTFmOqEY3qDWIV7osx3eVDvyP2lWjuB79wHC96QjT8//x3fgh/UDuN3Xv+Ef/r2BeBY7I8RYhuu5lgQSzhsMuDB9FYnUhnAnTv+mqfms562YQoR3QQXq+eBG2nc+jHA2tLVBQ4Yi37sJoJfkXPdrTjZ+6Q903NfbuJmTeKAEu/I3ZkwF4bKGZuD7RzIWmwcy0wGr4KMjN3yLKN/v7p2XmjYrFAQVTPuGh/+XwDw4fHIriQKoUyUJRkmUkHPxJv0ysHBtSiQpe3rRiJrvoTLMRwv4VyzBBHImA6rglWsvCXi4u470xTUdxfWyrh3adPp7KcjbAflJ6eBiOUofz15wEc7LHbQwAuYoztAHACgiXxl87n/DqYLIupoFo+lVf8QmFdrWz9OCAZhdWNmsex42Bx164UMK5UrSKnrfBVJiLLQyleJnk/vUB7690XCSLZ8otkxDHiKFJgwlQfQu6TiyIExSIqs6fR3rRJvWYGAbrlMkLXTTW5Q9cV521NJjdRnE2cZ0trMOdqQHcQjZnXi22bvohDsYNLt30DIef40mE5Gjl8H/L5BezO5wGLGuMjoidSfjw1ZfXw8SvgTizjG99axC/85z8EAHzorW/FW3//aryntSSoNTZ9UZyjPq1YaJVJSo5Gezj9IGl6i1b0ZDJzYPnjivVUbc82sOn/bDZB2BMymnYKSun9SO8j64BpLDlb49dLZPq5AfHM8vJ9dEaB4jHAG8XMm48n+8mSmChnae9NjqrO3K59ltwRv+s06sQIq1vhWELuWJ5Nl+vcanp/fxAdpwaPBXAlsR8gaVYkFoIcONGOA4m2RAhgVIoc6QywzTiGFUUoOQ7cgnB3tdNt/BA3eksAACAASURBVHPXx945sWC4oixKbLeMjGAyl1P8URthzyk9imfY/owxNg3xFzoH4D8BAGNsK8QY7Cs45yFj7FYAn4cYj/0fnPNHz3VixrngU1pnKoiyCh3VTE40uzKnxrMedPTsgrYRdYZbr6uyDQWkoFhck8XQqn89zqizmd4P0TUmhO61L0gI5fuw6HftnITj0PUsAMCXoCYzCOBd/iUAgPPYT6meh+kl/Z149RLh1CsH0o4gS7ndnMT2nf+AQy1bNJ9p5d4eRyd2MGecwhVF4YQeBsQobuEYjJXnIaYVtj8IL17Cj/zkq3HssUMAgCgUDuTG/n4c9jzcFX1N3FtYEs6JqCLkPaBwbG3ZKHYECWBXW3HLzCCfX4AXA8wWbTMeDKTHW2lfcvDZQKE7fiBx+r2kUw0/3QymZ9QZFSt8R+sF9WKrpetwJyEmLM0m6HB9/9gBLGDmzT6m/lgk6zN7WeLszUwgCuT7cLR+TlASQVzv8VAG05hMMiM9yFlathQ74HEJnr2sMgTXMBTZn46cn+12sct1VU8DENlESBxRJHIkjw05B4/FNsNk4vyynDhsCc6xUcvCQc/D494Gl55+ECg23jjnr1ln+0kAr9B+/wwEl/qTOXmqAZ2dUErRaQAwtFJPal/5vx50uGnCq1RUUxoAKnNzMOQ+tBLXz880Z0yr8265DKb1LvQg0UvPwohj1U8gjEe2nKQHO1PbrsgGaf9WSwUWfbLL8jwYvi8kWh95ibzfJDtSuI7+J4QjH3lQTDjRarJyADj9EyJY8KTkcnxJjq7azcRRSjqOhcUmFsgR7vyICCaL14oyni8wJnHj5fh47ev46ROfxdf/VayOr3zJNrz/v96H6RdtxfBLi0ooaX77l1ANAow5CaDKKp1UnEIofketWIOwAM5tlAuL6nXObeUAScoTADw5MRXoTp0cMVmWxsNqprMEp5ZWvQPEtaxmujcSlhLHHTvpY8ymeI4UTGJHbCMjx0wBwxtNvx6VRBAx/FTvA+3xdLYQlNKNeDLqIemBMNJKTVGPkWE9YMjf87kVhJypun7IObw4RpMx1WQWNPYVHOwkyPuSYaBkmilNdQCpMhKVnnJjBfzmVwpAexyXP38fbh7eAkCwBjejCGhehI2yHwSKC9AY7419oP6CTv9N2+lnCiJZMJs+OeTW63BWV9Voql7SovPp583yNAFQCnM62lrPcOh4ykr0Y7lpIpZa2HpGEJbLYn+NtsOS964HIBUgfR9dCfijBrctwXq9Gv70RxTieeJe2+NA/hjQlY4sEvKfhp8TZIQADK8MFlkyi6sgcunLXROrz5w2hRSJyZ/CwooqhdGz+cjHb8dfuC76X/ff5PFdXHPtOH6FD6Pyf+qYv1T2ZAClU6ArmLlEAIhkOiVvd9AJ8mh4GbyD4aPT2gY4NSHnCQBWE0GUWc07NTCzJbINPaPoBbjT+aP0Upc/KJ4jBQdAvLY6pXoryQfQXPuzPyiefzbL0LmqsqUgIuije3ClDomBJCgRRiUsAd118CJqeizT3KdFArEZ61mNLMmRw1ePTKLhdY2KkmFg36oQOqLeFpkCTdLvMsi4cYzhAdGLML9SB+rXAoafGoW9vlzGBywrWaBsgHG+YcJF31N7TgUKztLo617ypqYeCKTj0CeLdNAalWqAZIVvZWawaRIqa7FhwO/rWxMEqGms627T+XUVPEVLrgU+ulau0Uhds1CrqWmqFCmiFuh0I0lUIAlC+mgtbSc9DD0Aou8xmEvPB1v6ubXsuAMJuC+2OaRYHqJ8CKspqTLMwfQYKSBWsE4NQJqqxAwChLLMtvLFP1Pn/jyA8T6Gn3nx7+PunWIFfd1jjykCQAoIRP5HRpTkAISj9wcTp9c3k5TPVqfUuC9jATicNFrbHwR3/aQfoQWVcmFR9ET0Jjn1CPRxUlqFMz9VllPZSOQkTXnDT1b+mcmodSlEKFuhn9vjyf3SMZR96EGASmzZHomeJWQdrdkUQUKfejJ8lEsn1ep/MQwlANJV+BpAOPrJXC4VyEkedcJxEh1tLYugcwGSCDASdOTk7C4anMeRRfFelusX41Z2BIDoUdw8PIw7nris9zP7LuwHGcUFatkSDm3TXyPnr5hXkW4k0886X5M+bqufT88u9EwFSMufEsCOQG16kCLHqN83Hau/Tvehj8FSz0MH4On30AulThNNdF9Ou63oSOhaegamgIdmBKxeAhZ5alqKzhe6LozWUJJRBEyjN8kh7JM0JbRiDbRadyBW1e1NUyieSsCEhu/D8X34fX2pDEo8qyI+/eXfx93Dgi9qMQxVnVvnmQo5F7VtSWcNCBGckmmioQPuvFHxr3AMKM0qSdiQM4SUPdC+0pGWC4vSSQgwoaDG5qL/QboeJMbUPwOEJQz0zQEAlptbk4wsO41FDtnLOGoDgK+hw9V2zalnUeS9TA8KdEyvoKCX0PTAp+NRrGZSqiKTGUXDd+HmRHC2GMN0oaCyu6Z0rqQv4cVxyvl7kqNrQgO9AkhlI4B00rJsRSv7W0ZGcMesr8Z0m/2PAUBCDNlLwva7tB80sy9Ek+OxzDCg/zkpQJwMCtn+QHbaiAKIrk9N3E268+/V4AYS3Ib+Oo3Q0s/6ajzrBKnJzk0zBbjLNRprJrJiw0hNOOl9mDCTttN5u+Wy4pfKNRoIXReNbdtUM77XMwGEGh6LkmeixnnlaHDouoAnS19eXWVVawgSCZehj3QCwNCDaG2tAh3xRS7OTKrMSh8HJoBgcQF47TtuAgCs/tJ7EXzzA7Bayf2NvOQNaMYxGr6LAcdTjoR3tqNBOIqu5vxptR2W0KEyDTlebzS576IoFTU8MQRQdsXnZzGGTvXF4vXBB5PzluWkWHscyxRAskC95ENKfu6F29D30x2+rvGdRYfrNCT6aLCeEen3QqWvXrQlekZC56PMRe+JuFUMOB4IEnVNsYibh4exy3WVFjogsBKHPU81pQHhtEpysknvZTTlWLXu1OiYxTBUk1K3DQzjDkfK7fqDKtiM2baQ6s32lJ6C/SCjuEAty6AKJHxOWRyEPkWkbyPTewnkoLIssWR6P0Kfaso2q9cD8+mmsgZJz6GXpyiD0Kee9Pen8z7RMfSz39cHu9VKNfwtWaIrnziBbrm8JoOyPA9xhpGWnofKgLQgSO+3PTgonkn5FOLWNhh+0h8RgbiHgGJYAoxB0f8A0PphMcXkD30N/IlfBZAED7vVSgWQgb++DZF9VPVcAMD/2O8gF0Vo79yJ5effkzhvIHGO+XS5RDlBKov5g6KkQv9oX0JcByU05Dhvg85h+MnU1PI0lOyrPrmUxUkkH/7ajED/vReWQ/9dLxHpI7W9aEfoPVAA0I+n17PBKVtSo/M5taRUJp+Pa9Twti2ikfwaqw/tZoBwOUB/O8IV8m9+eEsf+IiFA50O9skFEwkW6UzAzThWzqweRYlgFeeYzOXwQqeIoCPCip23kN/yBXRkKY8U9BbrdXRWLln77J6C/QBwd4EaBYPsergXeV+WcC+7f4yza2lnhYV0Z6kjuIGE6C97LR3XUThzRm2n85IGhX5ePSPRm/B6UKHj9H5I4cyZVJOc7sXyPNFP0ejPAcCSJSnaZslGOosilSno96qz6RJ1SYgtYFGQUhckAaYoL79idlOsRmNH4CHIIUuHxisHUH7+xwEAja19MPf/oZjQarVSI8mWDOZ6VsWiCCOPPgp+eBKAqMmfvunBBK1NTrM0K64vcQQpo/1o5UwAtSwym1bYtavBjenk+HNlCVknrjt7OiaLrciO/J7L9ICQxWdk8SB6j0LPVOh//b56ZDX/8gKGB1pt7Ft1lPP/qbaBfX93BLXTHfQN5lAZEQuFq1+2HWM7+1OlJ2pwk2oiACU0RZrZROEx4Tg4faCGb/tNpTux+5pR3DIygvc9KjKKjvzcOls/hSs2P4GHT91w/s/tHMZ/QOFx4RlnLHHCmgPPUnhkewnrWXa89mymN325acKXfYhscCDHTI6ThIyybLU6lYgaf+2RjWRBeNkgxE1TOe31KEz08piOOWFRpHQkgHSG5dbrCsVN2YwZBGuCh0MlNF0mlp6lxESAS6Acl06oJWvIblU45Nlb0RiQ2UC+imhwHlF3EKE7pEpoeplQ/zn7nAAAC9eK4FSfBkY/J7bRBJKTQUX3mvrRyzXZ1WkvUF52m36Os1mv19crU53v8esFFz1jyQaq7LloO1F40O+yOf5Xi1/HYc/DNcUirpESuIPlAuzcNvzIT12Gk0e/g9AXWeNqzQO/fBDV5YSDiXAR9TBUTWwqMZUMA7tcV6Gtcz5Hsy4CRH1RLGhqp9u4eWIY76OxZCoZeqN4uFVLeMk2wH5QeroAjUkcBZBu4hKKOTLXEgVmt+liQal9tevoQSOybVVqomtS0OCmqTSxdVxDNtvIannr5a4U9Yg2mZTlp6L70HsBlKHox2SntvT7onIOHZPS+AZSmtyR769V4kMysURBqxe40JLvS58ui9mgCBwDjyS17tVLBFq7b0b1LdAZByY/gJdUDFFSeJHYvBiGaJy8Hps/k6DI1+PTGv1KB4CJ6su/mFzLhCA7DAbTK3dgrePUy0j6CptKUtnjgXSZhvbVf8/up1+Psoes4+4VgPRpsnPtq/+ujumhN6Lfp/7e9Huya6qMd3e9Dr70Qhwe+tr/be/dw+S4qnvR366qru6Z7h6NZjTSyHpYNvIDY2MZjLFj+4QYA04gwCWQkMu5IVwSTvhywuPmAQn3hkcu50Ag4RB8D4RLEh7BcSCBBAyY4DgGG/wEGz9kYcuWrMdopNGM5tE901PdVfv8sffatWr3rp6RNEISqt/36VNPdT127a5aa6/Xb+F3NP/Z9256Gof2TmPz+RdibNdTuPrlapU/urmO8XY7U7sCwPA/kUURCIGt5TJGSyVcWKngyC61QHj8qRk0piOM7ZpFbZUaV2u+g9XjOiV4jrEKHLxOZbRxF+Rxoghmn5aQTtZU8y1VXDsymWxlwY/h2+x4Bl+xuwLatmvLXvnzQLt9TQCZ1quu8yWeh3B+HuHsbMaq4QKfUn/5Ng4vikzsgAQ9FeHxNOOyHisJf86IG2jeLPvcSUkquvL0YqovTbQqk90k4gBAG+JAWgzVqUAFm1nPbMxtBVqjqHiHVQCTkcXtq9yFn1Qv7UoOyMPot0Yw/kqW6ilDJfDIrWQGogViWbvE4lrqdqGKcCDfynBZAdztlBdfsIOueaSE/LxcSdjWECkRSrGlz/wY3iCqPOVWglyBkRKLa2lv9eltgBfhN4eHDX/TlTecjf56iHb0I7zwpWvxvBdtAAB8p9PEjiNHTBwBUK6cuxoNXFOrmQD1ljBEzfdxy8wMHpqfx46yepY//JJN+Je/fgzPe9EGTE+o7LP7vrMXv3+DDzReo35LuqdAze3IqmcApJ3TjgcrGaMQQvwtgFcAOCSlvFhvex9yGr0JIf4YwJuhSKbfJqX8tt7+fKStUL8J4O1S9tZmZ5ai0FNhKwi7o5st9KUluO39ODI9G/SxFHzmrh3ur+8aphUw50yxAABqeOR5SKpZhs9OpYJwdjbTFc+41ah3t97PbnfK74szytL1ed0I3SenOaHtroC8IRNkdSeAyqiNSzxw3QcEC0A4gzjQL7AM0+rg8hSCifXp7nFN9akgQVjfCRy6Dt/ybsVIvWma1tzdiNDnx1h44UEM3auoOUjZ9cLo1y4AADRGRxENDCDa8FS2hiFDFKitmqChYhrELUX1CLbVQODpprZgt8n07JU87UupvC4qEC7sS+waNr8Ugfblx/H6DFIgLmJCXkPBlZUd+Abwd4daqPlKaXfqdQy+Yj2u1uyvn5pQcu/tu1Xx4uXVqiEKJKWx78gR4IhKCri8v9+wEA/6vinE+/knnsDHLhjE/7d+Ee+4VFkp1/RvBHZdpLKeYh8pXYGa28YKxhRW2PX0WQA3Avi8tb2r0ZsQ4iIoDrznADgLwG1CiPN13+xPQrVeuAdKUdyAJfpmn1mKArKrcIwjr76Cf5dJeWV0Gdy9xFNkOew4hm198AI42/oQbNx2thU/ptRsZtN2tZURW5YGZUNxhdWpVIz1w8F7fre1YuI1FJ4eK8UtjGIZUK4Cf0HXcfAXMEl7iWfcZ1SF50fdK9t2DZg7B9LXFBw6aB+XVqXHkWAbvwET89vTv/vGsVDbiXPOvxkHnnw/AEWhDkvR5aE2Pg45MYHFQ3VMb9kCjNydfmkHdCkllIjvuPB0WRN2pbQNmxvK3o8EsUtJANntLtcTgc+3vc2VgcXBg+kuNxRdm59r32vxiURRvt8xMIZB38eV1So2hiFunkqLCeXcs7HDfyIjrNqdfkWbos9Z830c7qgOddNxbBTFzsVFXPj8c3Dz09vTBkVjv8/qdPrSroKxskwXeAfFFcBKKQop5feEEFuWufurANwspVwEsEsIsRPAFUKI3QAGpJR3A4AQ4vMAXo1CUXCIXCXBFYirgU/mLMwdlLCMo3B+vitQylNiXe4proD4d6YuQJ9vYXg4E3wHVH2FK8idoRnR2VmAUmw868lcl20jAkBXjMNOr6XgNI2HivMA5RIr63ZTcUlk4hd0XQrSZ4oR4QPoU/GIcKZ78v0YMfWTLpWAvom0fzegrA+voQQBz5DSlCDj/gQue9WfAVBC5NADH8Hw4/tylTsH0bSse+QRkK/+4JWbU4Vgr/wB5Rqzg9Su9Na84HCesAWy53Ct/L2o22pYSkkEDcBjVg2RKLpat9oBfHtcnP8pL/C977UAgEf0nN1pZ17pv+dmtxiF21eeAYJ51bJWp+N+axxAOIWR8iI+dfbZuEUzCxxohag9PA08/T4c0ft6bYEkXFTW5+opeAdUICupNlLqlBXCUTQuWiOEeID9/WndS2c5cDV62wBlMRD26W1t/dne3hNnlqIQ+S4fvtbnxVuuegf6nwdcXam0Io7NeWPfN4FkF/2Gua4WvLb10X/oUFeWlet6/G9ACW+q3uZuoVKziebICMpzc12Ky67WFnEMoQv3DFeUTtttV6tdAW4exKbtnDxQDUACiJHA7862oj7YJCxKrAI4DlNXQamR1i9QJtTq+1TAuaqbJtX1/1rgLrT78IBUyuyGgQFsfMl/wwNXq7/v16GL0b9z8lJm5oMw+v0JAD46ldU4fJnixzLcTK1RVfPBK5W58AXU/0TN4UqldWUm5Ql7/h0J/pIje8oOXMfcyqhl3VScFZeOzWPF5eck2K40G3b2GJClIuFNnvQ5FhZXpYqVkys2tqIVPqooPPQz/eHNg3j14AAur70P83f9j+y1azuxfuPtOEAdE5tbgeZWw4ac3zps+TiKGMVhKeXlx3CJvEZvec3dlt30jeOMUhTE9WSnm9r/c3CBTMgUk1nbXQV3dA5ycVSsXH46NtOVzhKeNoWIyyohK4cfS9xRpWYTqFZNi1Tp+6hOTHTFFMgNZCufvNRhL4oQ1cvs+FQ58cA5BfWNskiECmT7SlmQ68hr69aqFJdQF0k7znHaCKptCKfSbnpzFykBPbAdI+d82QRLB33f8AVRAPSB+XlUPA+jQYCL+/rwilWaIuL938DNU1PY9fHeCoMjaLUwevd+mgUceu61SOoHlEXBV+tAll2Wr/h5O1YShO2atdpngewGy9iheXIKf7hpwksN97GueITterIbMLmsKR58d6XP8uP4dhli0yZFZ//ZLVuwc3ER7xsbwwGiLImG3IopCbEmCPD/HjiAjfpdOlwu451DI6gIgYjaB5dKymI9fA0OdGppOuzk87Fq717zjC5tYy6NE531JKU8SJ+tRm95zd326c/29p44oxQFkAZ2bWFP9B12dTR33SwHdlYVBcKj/n70M9pyUhw0BvL9izg2/nvzN7TSWaLOwcV2y2MJvOc1UWrwgj1Ds8Gua5ov6fnh5xVxrFxvvq5VaPab77galUwZmvP2dVJabLIgAFWRHUNts33+4VRWAJLA5XTbQUNlJnkRJva/2LiejtR2QvhNbC2XM+R/O1otbC2XMd5uY6u+98OdDv5gdBS/8osTqD6sMnXq+/fjaDDy2GOYeM5zkFQnAcmtoSjryuEC1hWj4EKau3B4fYIdF6D/XfEIrngIXLjbLjQ764krKnu8tjKxM7eWinM4cLHumX39wADuEOo529uxFBF9jkPsGrscqO3EXq1wHx18As9qbMeROz6KINaWLreY194OPP5uADCcZkSIuRKKAjixdRQ9Gr19DcBNQoi/hApmnwfgPillLISYE0JcCeBeAL8B4BNLXefMUhSeUNlHzK9OMP0omGuKE/MR7PqJrnRPtvLnGUv9U1PpeQHTp4IEM+c7Ih4ofj0Rx5kYBQ9Om8K2MDQpqDxATRxQfrtt7ml+aMici/ZtDQ46i9HiUsnELsiXT9dEsGBe1rivg7jUr+IGzGcdz50D+LHmgtKV2bMSUV33U+7fk65uo6G03SfxLKkJUv+Xp9LVuN9IO8ExJtTSls+jffjnlIDTbiDhq3FPx3HaoyKKTPAzECJtq+l5eGh+Hl+85kcY/YVHAAAvfjDGui/dkBu3siHiGGsffjgTF5rZdDY6A4tZiyIOU2ZVV1U0B1lVdt2GSwDnCWZb8PPjbfpybmHY+1AXQ1fthq3AXGPpNXYAew9eCgBYN7cHI9VJBEIY/idzHFmT0Iyw02uxujaGDoA57U6aq+1E+9sfQLk911WbFPtDwK7fxAuuUt0RH11YwML3P55beHosWMmsJyHEPwB4EVQ8Yx+A9wJ4kavRm5TyMSHElwBsh/J+/a7OeAKAtyJNj/0WlghkA4BYIn32ZwqV1efLjS++MbPSB5Dp75BHCc7BYwO8Utl2+9g9LPIoOoA0k4liF6Q0SEnYcQsSQG2WHtsaHDQxGNt11Ni4Cl5UNvEDcknxffjYbIuEz1dmTvyYFaWxl75/TxoU1ILFBBEBoNOnXta+jirEEuzY9pA6nlsKJBiG70qvw1fVhE5NFeARZYRWWKJvL7aUywiQ+oxHg8AwxnakNFW+FU0DMRgEpsL3cKeDnYuL+Ngdb0E4sRqrn3qqa+5c4HNGBY+twUGjqFHdn67yK+Pd6aVAdzA7L3bhQl46rX1eUgA8KM0LB3k3PZ7my+MvvdJ/Xc2b+Bi44uAxnMo4ROmIahxF56f/wylNLAhcXq2i5nkYLZXw+qEh/Nc9aoHwxDc/gBJryAUgpb6pltSck9vyyDagugeVXcpj03r30A+PMW6Q3uZFa+XATa9dcr8jl33yuK91InFGWRRSs8d6lhXA+Y1cSoGnowIwaaw8IO1qMESreDvImyBtL8otB0/XR3DqcKM4PM8ohVKzidbgYMaVROcKSEmwWIL0fdT2OTKI2D1y5MVDklK6qPBbWsiXmeunshNoblUKgaizAdMrIamzAq25c1RCwAIQe8xyKE+lNQGkgEpMcPSNp8KlNZql9gbUfoevAao7sWndj03GSc0vYzQIMr0KqCFOzVPtNmnlF3ie6bVMlb+jpRK2hCG2vuxz+N1dkzh4qY4PTF0BbPksRv/mzbnzaycHhLOzpugvCUPMD5XRqYUAmGKkgLitFFyFcRyuammX9ZG3yucCP5zqpuHgVoLfALi+si0d+7ymIdI4vnGpwKufegrtxrlqG8VbSLmzFqk138dcxM5bGUfJ62BNEGBrWcWbdrRaqAiB3VGEW2dn8cydHwMA9LUmu1zNPlnyWz6bUWLlnc9Dac8IgpZyPa1E5+wEReOi0xIu1wqH3UqUVtI8lhCw7wic1I+vxstzc6a2gisSsmK4VSN8H+1qFbLV6krXTMIw7SXBKEDsmIot9FuDg6b4zlVYaLvSAOUaI7vIy8RGrBRfGab1AgD8yXMRl3yIuK0E+pwVbAVSKyNYQNLpAzxP5a/7je59ibl1IXUrYWFUWRxAlg6DC6fBh4BoCPuiKMMFtDuKjFIgTMcxWkmCQd83mTLTcaz6VngexnUwvOJ5CDTV9ZvWVvD3wcMAgG1n7cT9O16LQ899LtY+/HDXLXBLjKcD24kLXlRRvcDrWrlOb3MHkQn8u6WsC1cMIi+dV0QqxkPXsFu0kmIOGunvYI/BZSV4Uar8oiG8/McNoD/IckjF3QqtHiRpeqne1ufHqAgP19RqhtZj5+IiXj88jBsPHcKRp/8zyvr9ySgIRoUjfV9ZnuM3AIeuAwCU51RcOC+F/thQUHicEAgh/hHABfrPQQDTUsptjv12A5iDCn12lmO2Cd2Qx0Xgl1fAxmMEQLYDHe8tLeIYUlsV3DXFGxIRSBnFyLqxXA2KRBxjYXjYWDCAyioiF5OXJEjIGqJGS1Z3O8Mx5aAB4W4u2seud6A5CfjcAAiaWmm01pp9fbrXuXPSF7Ovk9JecBdTsKBe/pLlG6d9SEFwJlYZdgs9W1FEQ0DQgDzyAizo1eJCZRylcBotz8v0XgaAiu+rxjakFLTw2ddumyrdho5jHO500JLSWCWPLiwAnRqSVc9g/HL12K59eJfJcLOr1gElsLjL0DxfCyNKcAFKSM9b9QdkWdmpsy4SQrIM7LgDfUfH8W1epIQ/dyHZFdW0n00/bn/vAvXwcBEL8iB50IAoK6HdkUo5B6UF87vU/ABrggDTzOLbEoa4ZWYGR574HVR2bUI4P2fmn57nDlPYcakE74cfQd/kJErNveZ3WazXUVkmxctyUJACniBIKX+NPgsh/gJAvs8E+AUp5eFln1yItJrY0QaUKwAC+Tbt2gAAXUVkrrRV4+NnSoWvKnmWErmqbHoNWgFxHyuNt2NZQC7mW+f3NGarQ5jNpJvQNuveA0bFwbOaYgChVsaGpmMhAJAgBluBEiUHUYjb4CvmtuZLsleqJAR5DwReb2EJrEB3OpvWY2/p7mnUi5lWpy0pUdNd1XZ20ix4oofYvbioWmxCsZU+QuRymn58essWDO7ebZSESViw5pbmjBSw9H0InTkWl1apgkPfO8d9kAAAIABJREFUWuG7+k24FAK3GmyBHOg5JyJFfj5XphSvxbBdYUtlPtnnp2NElM3AsuIgsr0aALAQNFDyOhlLcI2OHQ36Pj60QdWKjT78MNr7XgOsuQvhY6/KvGuUKMK3lefmEGjLnbf7LeX0hT92CBVfOc1xyikKghBCAPhVANet5HlNWqclIAGYOAC5faR2BQGMq4g9eL2uwc/ZKwZgNx2ia3A3FtUfGMuBxUxs4kLbreG6R9c4+fE8E4r25l35+N+85SmvsAaybVel78Nrp7U+idcH9GkB5LG5JN93p5a6KkjgBY201wNtF1F3tpCwBKbedyH2UQ+StLd1oOmnY9XohrOTUuyCY18UYR8U15DJ6fci5cKYuCZzf7xLIOe3Mv5xtl/QaqkGUI5nRQltrQhlI71XuzbBtqp60YGT5cC38XoOu+bCtih61UbY1+uVEssVHz8vs0pISQwGgRFWrSTBvihCp1TCbz2jCPwGfR+HN/wz5OP/D4Du2ijOQECWr4uyR/o+PMei8JghxfITD05hnLKKAoog+qCU8smc7yWAfxNCSAB/vbxy95Rm3KajIMEv/SzrKaeaIHCiPFdHPBMYD8PMatymC6dmSQCQxCnxnt9uI9ZjIAsjU/PhiHFwuLa73G12fINvc7nf7PPZ989fSt4bw49jQ4Fu4jTVUiqc2rVugULKQt1wNhuIQEKmNJ4qFV6Exl/Q+c0Q9cfRkZ5JlZ2YeRbQvwfj7Xls6+9HzeEiIOVBLo597TYOTG01TKiYvagrsEyBalII9He7WkW7WlXPG0t1psQGNS+63axNVU73S/ULLoFsZxeRsnDRbywOoasBk7B+A9stRCiPp/28bWVBKbyu7/gYTJquRVtu3ccNAwP48oYt+PD0BG6dUc6Fu3dep5IIvCi1RptbgXM/jXBiNUQ8menwKOIYrWrV/B6twUFlOQCZlHFS6OQuXhFI/+gaSJ2iOCmKQghxGzIpHgbvkVL+q/786wD+ocdprpZSjgkh1gL4jhBih5Tye45rvQWKKRFBn+K+t1NASfAT7LoJO+hsvrdrMdBtTQDoMmVdDY/sgDTfTvQXnIOK9/Z2UXfYgt23lIKdusuPyys4dJ3fZVnZWV50n5xBN2i2kYTlNJPKJq7rYytW7m7xkQo0sjqSkAXJ2Yqbu6sAyMV1WLDz/KeugOzfg0fFPuPaqHkeNoYhgiQxld1EONdKEuDADaoXhoZqNOWhU8nGloidljPxUqaacSNW5oC4nLriCBSL4C6Zyri7n4UrLqDjNEYx2MrCb2SVSl4Ftu1q8iKgszVLQQL1m6xe/z0cmd2SBsB5lTkdmwfbVaaPebTVwpvG9+KWmRnMjV2v9p3bCkRD8FsJfO2iEvE88KP/jE6l1CX8pe9jYXgYNnOxnQ1FfydLJLwcHQqL4pghpby+1/dCiADAawA8v8c5xvT/h4QQXwVwBYAuRaEtjU8DQGVwq/TbbeVTt1JQadXOXTk8q8h2xQDdbiV7dc7pOTL353AR8WvYq//Fet0p0F3bXOMAUlpxkwGCVHhz15FrvJ7e11VvYbvhOG0HV5T2XPg6EN9BJa2tIJQcMQtKmbUzdKh4jbYtjBoWUExdke0FEYfKL0+NaYhxNRpCu1NDW1slc0mIjlRuI4pfdKTEQuwDs5cAcS21DiuKDJKz9vIAqp1WnbBaFwBAtColP6SVNt0v/Z+3QrdrHvg+XpQWLHLLQURAmBPgtjPIyCXlM2UVNCDWfx1y8mqU1vwA7YMvUtuH78ORxllZeg07JZcUvM+uZTPv6t+SrL7DHR//MDkHPPm2VAEloV5ohAjmskHrvsnJrphcAsX+a5SztvTpGP67LZUVefQoFMWJxPUAdkgp97m+FEJUAXhSyjn9+aUAPrD0aUVGOBvXU39/hura9v+7XDR2HMAVM3Clr/J9XbESV8V4r1U/z+JyuYhoO/Et2daCa18bZMFkKEIcCoq7nMgS6zUPqWIuZ2o0zGqYB6nJOuA5/V4E+OPZFbMfAQtD6TYuOGmlyrNv6LugkVollXFMLNTRV55BhSwgIdLzhVOIK0poeW2RLhhYR76g1XJakoYBIFBNdFCadscCiBjPtoDMyZigj4ZS7ibaxzQYqqXUJ4Q4zJ6DlIGdTWUa+jDrIxqC3PvrwNrbUfE8tEfuSsdA7jIO7s6yYx+uWIZWHhQAbiUdjJQEJvxIKVUzl/MoM6XABT+3EjLf6feEmnjRdn4OYOkU+qNCEaM4oXg9LLeTEOIsAJ+RUv4SgHUAvqri3QgA3CSlvHXJs4r0ZeWpq+Rr5+4lAADrCGe/9F0uGmbW2oR/BNuCcCkfe+XNV/M8o4n/bR5s7SKzO+TljZkEP7mIaMWVp9jsbB3aZqsbyt4y18lRXplrcYFCbLG8DmPqCvXClVisQmqhH06lMYpOTa08KRPIDCpKz81rA2ilTNW5gFlVL8Q+9rbVb1YK5lGvzGLu0GZ1fEwLg5ZxMdEzEGgB1K5WsTg0ZBYDuUkG3L1kjSGjKDq1rFAnUKyH3xc/3laYAFQbQTY3cQjEQ1kyRgo2c+VB4zx8DeZ4jKC6J92HH8/u79p1KuX1zslqNgZD4BXZWmm3AUx0aoqTiRR8OIWo3kDlJykZJRWmuppxeVEEj7lCSYl7ul0vj2cA7uf12OEViuJEQUr5m45tYwB+SX9+GsClx3JuUhJ2tTVvE8prBWg1zGscyBJwZU3Y1wK5dyxLxrXyJ1LCru2OlSn5Xm3Xl00mCKRKzL5HexxkVXGFwl1vfDspMD4+HnR3ZfC45oeSBYzAGL4PmLgGWLiEKUYtCEnIl1jMoqRXyxPXdM1bJpvKj9RxPLunPJVaHpx/iT4zEr52px9tsnRqOzPWThKG8KyGT9JXjL2L9Xq2lsaPgXAiHUdpKm3KZGcBUeovreypniRGynNFiLUyWFBxONR36RRUZpURuKuO5tHAEUfgsZ7KuBproi27sjVn3LrjsZQkxJ0Tq9Nz8liS/luUjuDivj488syVaTOh2YvMnJ935f8FABgMAtx/37vRGB1G3+SkOSVZBzxGQc9jODubWZyY/Sx3k524ctwoLIrTD4kfgLh27MI6wC08+XZzHkbRwR8+EtT28bbwdQleGoedm5Qp6MuJh3CXmV1QaPfmNi+Bg2YdUH0mOEj457nJMtciChJolxjb155Dnkqriga1YDh0nRaCIbwWpdeuSl01gFk5e20BEQ8irs6nfSeChkpX3fWb6m8SyP17gJmLsu4ZogvxtKDmwXOySDi/EHetxOT6UwoiYy1EkUk2qI2PG0E0s+WsdPVOAjauATJKXW2kgIg6g9OBt5l7rcJccxSLiFYpBUHbqEBRMIHukfXAxtCuqf3IxWRbD0BqydlFj3TtEpuzkO3L6zt6uZz0/zsXF4EjV6TfLw4BZ30NI6ufxHhHuSfHOx1g4z/h5Zt34+s7/pOakt0vVV0ImQvQXILcUVZPeNvyJSXhqpk6Zkgvv+XsaYQzSlFAwKS+2plFvFWnrTi4kMuLA/AgMUevwje7psHl2rE/8/3tzyTQ+WrfmZufc05yZ/F+FJSe64ozeLoHN99GAfM8ynNb8SWep902er7CEEmsFIOXKMFAzZW8qIpOpQzlkGAZV36Uxhd0cFrvkAq9mdRt0eXuIFcJrdzDnOycOEwzj/pUT+dOezDTApbu0/ySYWjqcvxWgrgSKlOVC1g6d/+erGIi5cWC0oZY0YoHBLNldAZmWHe5ValFFiLd1290U6ZQsDsOlUTQgv6XL7oNX3/yeep7TsQIpHPoW5YJd/nx/7l1oYPVMq6iFChFO+j7aEkfc/Nr1O/BssoQDWFisWwIADsAzlu7A6OlOrBGxUjk3l9Ec2QEq/buzfxkec+5/b4B+vlc8WC2152GfBrijFIUQqZ1FJl4AMvx50HYmAlgXqnsErzcouCFZnQ8gK4YA6zVOKDdGBYNun0eJTTTyvKAbXeNzdy/Q/nw4jqaA3vlTxlMns4WozFRfILfLw/m2+SIziwvfZ5oRPVN9ebWq/OWGhBxmpXWrlYz9QaEuOLpeMY55n6S+CK14s+8oEzQDWg+Je5yElHWpcWzrAilhnKFzG82SiWueEiaqtqf5sH2k/v6/5HHHsPchg1YrNdTJReV1e/bNwHMXpCpEgaAUnOG0X10VA1GVa3evabqqOdFEfqnptCZryAuUZyJWTp8HmLtTvOjLI07ZVytvR0jddXe4OvbX5XGBmzyRe4aA7KuMDtJQKOuBX0rSRAID7VgEYFQIujA/mtUbUpcgze3HqXmnJnD9hOvR3zWVhyhDDYAW8+5U1Gx6LqZcHYW1YmJLqVNsJ9pzn5AWE473KNH4Xo67UAd7gB3URqQjR8EbNVLIOEofT8Tp+DnzezrsCh87Zf32+0uM9l+ePPcTZSLzx9u7iLKKBp2Ptt3G5dKkDlpukCah051GLbws1vIcjebyRojnzCQqSmgoGLU34/yOF2zifLcHKL+fgSt7IvLK+Zp7H4MiOZ6SL+d+c7wSNlIQmBSuzaqe1L/u4esawfIup5IMNZ2dhHltQYH0RocNA1vTLoskKm7ScIQtfFxVKanjWVL9xGOtZF445nniFx5dN9ekqiK7z3QWWxKcM4PDSHq71fn1J0CTQU7WRAUu6B5sesjAi3o974WE2bCG8DYK9OAOJ8HAqeYp9oVonb3mwiEyFBvAClv1mipZPibDiyoJAGvVc8sNohuo3XwhUie8xdqYziFB3ddiwcPXoehHSpGEbTGzHPH08DpebcXGV4UqeeHbSMWBJcVcswoYhSnIaTsSl/l/9uuEq4IYoci4MdmAr3cOnDw+9DDbCshPoZeVBvcl5r3neu8ieel2x2V2jT2TE2HngNX3MZVLGjcV9y0Z3QfBIql2H58qlr2kqSLOI8H62kb9eXg86tSVvsAn2Xw8NoMF0VFpqqZZQpxfz2tkCnDCgCSNH5Awr9TqSCsVBSdOAty0zyWms2MwqSx8/7lFOS3s9Iq09NmLkzzKACt4TqAOK0byVBtNLL32q5lYx8+c3+VWVyiY8VtANTP/XvcsnUrfmv3bjx5+NysAgmnIPqyrp81QYCOlKj5viFh3FgqoSMl1gQBvj62Ru3Y2AokKQfb4oCqranuV4WLlelpdMbfAACY3VIFhu/DwO6UkZms8EQnnthxCDtoTc9p5r11pNYePwpFcVqDC8O8tEWeWcQVDME2Z0nAuV52l9uH4glAVjHYAXEutIHuynHn2JnC4T5zO212qfgFf3Fs95GxyhzXojgFjcVO5e1oZdnRCsVlOdmBRrJKCPz8XZ+poRIFyRdGVJMguy81D7iSUuHMqBS34MR74VTKbIswdeXogLv0A3MfPEEh8TzDMUQ8UPye7Wwznx0HwAi7TqWCdrWaeR5ky1duOLKKKuNppheQbk9qShlkUmbD1Hrq1LJNimi7VjSNOMZnDh821CbvvFApzY/tHMLq2hhqfmjoTlpSKuZXIRAgpUNZEwRo6UZRI6sUV9MEAC8qw0ta6IQhsFr1sfZ3n2fmg+ZhYHcTs/F1aI4kqE4Y+8ewwiZhiNmzzgIADO7ebebOFUuzU2rtAPfxY+UUhRDibwG8AsAhKeXFetsQgH8EsAWqw92vSimP6O/+GMCbofLk3ial/Lbe/nykHe6+CeDtcokOdmeWohBuPz6tzO1grekXzWIUxmXkCHy7gmO86MwGtzTo+q66Dds6yBPyLv4l2p+7hVzn4ufLuOWYEHYVK2ZWYGFogoGu89pWVxKGqExP51onvDYl0EpXOH6LuFRCic1zp1JBAh9eu87mSiBpjSqBSRlSXBDyDB+eDsqzhRZGlfBNQtXzAgDmLtJ1FSHQ6dMn0GnGORxdSRiatE6e3gkAYBk35pnQCoGEHfU3IUsj/V2riCuspqLUSBs9kRXlMxoQ2zXXvydtRQso19XA9oyrTR58Gb5wENi06T9w1egefGxMfxGEONIaQKs8gy0sO26Q/Z6Gcdf3sUa7pAwFd9BA0Koa60HsVw2N/HbLWAv9U+q3SDwP5ek6+iZTTifO1QbAKBBSCNL3nV6BJAwh9W9U1rUYK+t6WlGup88CuBHA59m2dwP4dynlh4QQ79Z/v0sIcRFUPdpzoHpm3yaEOF+3Q/0kFK3RPVCK4gYs0Q71zFIUyLpMbJoFO/2THi4uwHmtwVJZSvYK0RbsfCXMj7dXNGacOULe5fpxgafO2lYOAAhWvW1nfhnqEw3bnQYAXquVa53Z9+632xn3m23puBIIbKVL9xNYc8uZWDPxFvhAu44k0sww9V1KiA5sVwqDB3c5+R6gAthzW5WFwtMdqZdGHBoqjrg+BUxtVBbl4GDGugtaLUT9/WkrVD8GwimULv5TlL/+XnPa2vg4miMjCOfns5xZSCln6HmlplnS9wFfWyoUM6CWsqQUajtV8SKQCjChraTyuHIB8fvb/8qs227rjUASopUkuLsRAZFWIuEUhN9EK9EprlCcWaQINoahiVHUPM/Qux9pDZgxkPITcVq3RDURXIDH1SoWzzqMoFVLn0FtbVFiR8DcyhRPpGea4hCSsfjStcIV7EWhBiC6aduP9VRSfk8IscXa/CqoPtoA8DkAdwB4l95+s5RyEcAuIcROAFfoPj4DUsq7AUAI8XkAr0ahKDiEU8DZAsWV6mqvqu2VOwk2Vzpq3gqFWyF5FeD8O/O3jhuoBvFZHirTMMcR6wBgKDZcioteKhHHJlhN1d6ueIrr/EA2/kB/x+gxz3GcCerb1p2XJMay6XID6rmgpjRkqZBi4wovqR9QQjPU7grqidDYqhQDrZz796T9Gvp0PKI1mha8AYZOwmvVYbiqKLtovgaVsFXN3If0fUQDA4ohdkEJqfL0PBbXAu1HP4D+dsushONSCZXpaZO0wOeaXE9drs/KXFaoi0hlEoVT6Dv7HwEACxNX4XWX34Qvb7+mu5J7epuaj5gpitgH/AjXvvDDAFRv6hsPHcLEkQuV8tQxEdG311C1U6fAreUyLu7rQ83z8MD8vFEaOxcX8Z17367mb249AKAyPY2g1TTxBG552u6gUrOJtfeGWKwHmLpKxUQGHjxPn0NbGHpuOpVKWoXNEjn4woSOWdnYBEGc6PTYdVLKAwAgpTygSVIBYAOUxUDYp7e19Wd7e0+cYYpCwaR2MuHMA6LGwmD72at2G9z6cH3HH3a+2rUD6c7xamGYF4/gL5UdtM6zaFwuOFq12fdqspgsi8IuJOTfZQLiXnenwLwx0DXtVqGu++X/23Ecp2XT1O8DZQC1tb8+0UVmFLuojCu/PRWXqRNbxWjKekiSEP5CoK+v4y/VEoJmmipLd2w4niyXz+DjTUxfIlGdOJIJUAMwVCDg5wAyVgYpz6TEGgFVxlWNweFr8OuXfhtXVtW97xh+AlvCfnyZLCkgVZQD24G9r03pSZIEiQegNGUyl+5pNNCe1UqC1UxIWcKVtX404hgX9ykX3JXVKlpS4lMTE9gXRZh48k3qetGQynBqC5PRlbH8WACfMuOylqGyrkvNppnL2bPOMtYAj/25Ej6k7yPRLj3+/coTAgJHEaNYI4R4gP396eW1Tuh14S7IHtt74gxTFDKbHZMT8LUDrx6Q+Y78zC6l4Oq5bftI6dy2z58L0672pMhaHTzAzGsblhvPcH1nr/jzjjPjzzmP7cITcdxFOUL36RqDK5OLX4ef11YaBFvBZ+aFqrwpM2h6G9C/x6xuMbdekRT6jbRQr9RQrLMU5yAFIqK01asWsJXJaSPgEs/D4galmLx2ovqEY8g8W5XpaVQnJuD9eBiN0dGuxQtnpeXzQbEYM79JgnBuEVH/SHpvja3A5ptw89QR3KaF6EMXXYR6I8Gan3sAdzSUkP/C+HZcu7qNO+/4qL5WGmdKBhYBGRoLAECaJVVqAIc1dUo4hW+NKWV6p473fLJ/j3Jpjb0SaG5OrR1dt+IdOrsrkEzgKcH2d/Q8Bb6P2oOX6P3GUJ6b63pG6N1NwhARdRqMIgRs8bLi7iYOuWyup8PLaefswEEhxHptTawHcEhv3wdgE9tvI4AxvX2jY3tPnGGKQsHlLjHuG25pILUqbP94XCpl6C6M64n5V8nfCnQLTzoyL13Xzhji7iCn8OP3p4v2+L69FAZHXtDd/l44XHicG8seDx8D35aHTA8Qdm1X/MQ+d959mN9WB529pKznqQ3Z2gipD1HuDh/Sr6esttGQ8u3HyspIu9mVtSBLBSylvJYnJ9EcGTGCNfGB8qSHyvQ06vv3m3ngXFDNESXog1bLuJ3o3sL5edPPIhpsqz4WgDp/+TCQhBi55I8AABXPw/X1OkZLZWwpn41RHR8YkR6m5yO8et0g3nLzH6jjB6bx/eYwgqjVlWnmN/sRM9ZWZRHx1Fqryp2lD5cqh9CeulwpidkLzLlTV0/LWFCdS78LVMax7ivXZOJTpCRcMTW02xh6+mnzJy0c+PPqcgVTD/r5UR9n3fOUeRaTVquLQue4ceIpPL4G4I0APqT//1e2/SYhxF9CBbPPA3CflDIWQswJIa4EcC+A3wDwiaUuckYqirw4AK3ynZaGFUOg1Qu3CmzWWPKPukBpfNw/Sufj6aQATOEVoVcmFZ2ryx3kcF/ZQtZFtZGHPFebK9sJSK0iGzTHNA+U1SN68FW5zu9yf3HwegY7HiTiGDJJMlxAnulRwpR3PKIEpd9AAh7Q9oC4ZLJywtnZjFUaTivXUX3/ftT370enUsn0RogGBnTzo3amurs8N5ehUyGCQZV1J7pqREYu+e+4UJ/3zjs/jM+3dHbYhZ/HF5+nWsuHDxzAwLf/CwCgUlIFgotxHZ3L/gLJoevg7z4/XTSRFRzOZLPA/IYqVqQCOwAv2LgdDzSbWBME2FJWCuz+p18KTG+DN3M2Ss25TNW5iGPMbdiAZFA1sBy88zL0T03Bi1JLgpC3GLC3cTduzD53dK0Nfyai/n4M7RjLBM6DVguJjmesHFYuRiGE+AeowPUaIcQ+AO+FUhBfEkK8GcAeAK8DACnlY0KILwHYDsV68rs64wkA3oo0PfZbWCKQDZxpikJmXTwcVHlsu6bsVTL55TkzLOBe3fM0TleMgKpDARjBSIrJVgbcpUU1CHlZT7m330PQmvu17iNPadgxFro254qyj+tUKrn1KHmKDcj2vgCYSzBJWXnt6nkaozkvr9a1rm27NuhYL0lMum9cKkH4PmJfczVpBQI/ht9KIH2RcQdylwoJyOrERCY4zb+nZ4QHs7lFSnNCK2svYj082jXVQ6M5jMkfvFcPK0Zcnce1P/dnuLivD2/YqRTlqm++A367lalK7lz1HvzhWTV85IltEPFcJtssLpWUkujThXwiUkqithMIGjhvSMVFv3/us/H7B8fwqYkJ3P+0cke9/7JH8N6f7EFw8Lczc2LSXQ8dQrup6h0q009lrHpX0oMLXbQ4yD6zGYtaPyutwUHEz/oKOlPXmmMBoDkygtr4+MoGtaVIn5XjPZWUv57z1Ytz9v8ggA86tj8A4OKjufaZpSgEc+s4BAvgDvry/+2MCS6gbOZWOi4ulcxDCqQVuCLOMlpyhWI/qjajJWX3uASkfX0+7rxKcA5+H3kuq7yXkortXL5iz+p6R4hLpdzKd/vafC5dwfckDBV7a5LAY4FK133w4D93dRnurzibbJAA8FtAXOoz4yeGW/77kBL3220MjI1lrEZKa+Xp1l4UGRpsbqGSsiTFYooO2210Rg6grKuaRSzRqZyNgYfeiKlzdVHa+Dha7UHcee+7sP3haaw1cawmvCTB1HlnY/AplTGE8RvwkQdfYrKGiO4iGhBAeT+w5bOmN8g7L1EB8IsrFdzTbOIzh1XGV3hHFZh8AzC/Gf6CEisf/MnL0N9qIWhNm3Hz34JX3/OFDwd3Q/VCV6o5++xFERKWThxXPGDPr6H/0ENoV6tojKrsL4oXrTSWM/4VJDY/ITizFIVOjyWYeAMXJpbv3SmI0C14SGnwfYlKgGdxADBFfEQ/AbCVkZW1Q1kZPGXQCFMHe2ueBeDqyEdj5i4Y6IC4neGUF/i2XUo8A8sVaHbFevjfCRP+9nd5n/m8k/Cn/+0EApkkGSXMM2Q49QqQKgdCp657W6ODRLt7kpLq3cxrTKL+flN5zYPR9DyUms3M7+6324j6+xENDJj6CnI9cSuM3FOV6Wksrl6PxVHl6hp+aN6cd82OHWZu+g8dMtcwz5P+XdY9tN0ooIEfPgdetNscR89qdMF3VSB69iKct/kOAMCgP4ya5+F9Bw5g79xqoPMsPTk6g6xvHLFuMCSO1M0ck0Kke+tUKoqKo/xM+jsk3dT3mWezB8h65G4zQAlg+kxcXFSvEbRa6ABmznm3uxUDIyI9nXFGKQop0swwLgTsTBvb1eGKBbiyc4Dsarw8N+cs/OLZKnzlQ32kE88z9Q5AqixovK4qZvDvPC+zeiNl5fLzc2RWs+wafrudqQKm7ZySAsi6i2xrx0Bv49XGXpJlpaXzGOoL/b/L3cVX2XQ+goizlB90vHObZUXR/fGge9BsQ/qB+k77nf1WYpQBrxKmlaz0fWM10v2FrTRoHJdKmboIinPMDw0h8VTgmwK+xPPUqVSw5tFnUqvGYhsGAKnjXDQGzjBMHRBNPGR62vyuMVLrqPLIL6C1tgHvmVdh/KzbAADvvfslKjYxeYWKjWy+SV2wNWqYXCl4S8KY5oYrgfLcHPzmFsS6Sp7GSp/5b7gciDhGa2QEcxs2YOSxx9LjmOXG3cfluTlDiTL8pIqTTF73KII7O8u63vJRKIrTEDJTZ2Cvju3P9Dfgdl3Yq/EkDLMuI2s1xFfAdgYIv05gZUIRJbItDGJLWbncOly42srR/G/tn4l/6FUe0WWYWpBY9ccWOujL78VuqWrHeIDUj9/1EnleRlDT/WQK5xyK0iglRmLosq64ouEEiDxozBWErTDJbx/XGSrcAAAgAElEQVQ00zx/SmwwglundpIbjI+RfkvjjtLPAi0GpjdsMOelfRsvuBsAUPv6OVgYHsbC8DAGd+/OCFa6L2Ntsrnl90z3M3neeRnrgz8jNGavUgEu+DiS7X+aTuDiUJrBtDCIeOyV6XftGrwobU/qJQsZN6Qdg1i1dy+mtt2qv/tPPRVEXpzM/nv+gp8gfiKl+jfHlkpYGFa07PTcUSEn0ais/fYFAB7rus7xQEi5rPqMlVZPKw2xBBfUzxTCkYvkyGu+YJSEy01iwxVoJeQJs14ZSwBMtpMd77DPaV+Lj8nOzLLHyl0bXPC6gu920J1vs6tWu+IF1nf8OjaBoL1C5ym8thvJ9tdTllhmHktSMcXq/2m8pIi5pWHPG58DcoXYc8zvlwjnSBjT2MP5eVDv5e70T3U9qgngyohA9xmXShkqbFrt5vnu+Rhdzx5XzK3BQeOHbw3XMfrDR7rGwEHzTll7calkjo+Hn0Y4vikzz+Y6w3VUJlMG3Mr0dIa5lVu5nJTPNe7lrsJtV+/BSy5Ba0MTG+4Yy5zH1RKAYjLcSq5MT5vf9tE7/vcfHmNtg4G38TJZ/r3bl9yv9e6h477WicQZZVFIgYx7wc6scK1AaRs9yFF/vwl8krsIyApmLoRj7VJoV6tdgoSn4tpU2dyX7/LVd9jK2WUB8ReY4i72ypzui/vAATgVim+9wGRhZBSpdiHZBYlG2DECNi4gYj/bu4LuJtYuFzpXqdlEu1rN9KXgvE50LVfKMq+KJ3CfuF3z4ipq49YDUYpH/f0IPM+4WfgYkjDM8F9RgJ3HpriA5+cQcYzG6Cjq+/d3WZKu+JjJ2mNxlk6lgubICCrT06bewNvRrZxhLSYOv/o+AMDar19l5obmPNkbIvEOmWvQ9UqAIXjk4yIlYb9r/P+ltvcC/806lQpa5z0ODGzHYv1qAEqRJ56Hxuio+S3Xbt+uFHN/P8LZ2a4U9ZWEsIp8T1ecFEUhhHgdgPcBeDaAK3S6Fn3npMa1js+l1u15Xct4cq0uubKg4GenUjECjvvCbT88+X+7lIausHWtxikeIn0/I0Rdq/EM6yW92GyV7XrQl0rftf3b5PqisQb6PkmQuFbEHKRkJIsxuF4+vrrkgp4EbOJ5pvbB05xHJKxtK6FTqZg4gN9uI4xjzK9d22Wd+da16d5tt5iIYwg9Jl61S8FQjlV790L6fiaADaiAqbNCXc8N2DNCWVa8Z4KIY6x+6innHPcStLTvnmtfCGy9Eatue00XpTkAk53WNT4AG7/4HH3dplmomEZVfLFhxa6SMMzE93ixqB2D6GVJ8EUGHZuX3ccXfnGpBBy5GNh8Ew6/WFlAa79zjlIUL7gbv3i+oj76/vzbkXgeNtx/vzOAvqKQJ+i8P2WcLIviUQCvAfDXfOMS1LgcTmrdpS4qRX7eNc+ZJ5hVoRaWQNYa4BYFAAi9WuTHk3Bt+35XNzouAOgaLjeYHcTOOwfdi2v1RlXmtqsrsVf5OkDNV+D0snZlEFnXIivDzkDhY+H1IqZ7XttipmVtRfn82PETOg/QzX1EPn5SNi53hz2PXFnROei8XKnEpbS4jrqi8TnN3C/7jRYGBtA3OWkUHh3vJaqiP3CsPPlzSuhUKoYihO+Xgd9A7bu/hvr+3U5B1asC2U6NFta5zQLA+o3IjUPBdy+KTGKGsJQ7PVOuZ9X+DLhrfGx0KhWse3Anpo/8Nyxe+D0AwMymTVhcHQDTZdw6o9ac5f5+DIyNoTU4iNr4eK9THj+KrKdjh5TycQAQooufykmNC+Bux34v0p85tW5PCMmyYsKwK8DnegxJwNC+lK5Igo5TPdurfuJDEnHc1ekMtoXgeWlevzUGekm4m8oZyNWKgKsOXrjlx7ERyCTAbMXkJaqJED3atmDlAWs7nZQrlww1Nos72Jk69r36AMTsbKZqnXz4dtyB7jtg2zqVCma2nIXytGpHyq1DILs6N0pAj8PsizT7h7sljGWHbAxHxLFierUErFFqbep/3cxcj8YufT+z4OBwPZP8WTL7kdLQ/2/83uNdtTccLmXrumaCLIuy1O5F05dFg+amb3LS3Ce1u7VjLS4lkXGF5ozb5cKhZy/q70d1YgJBq6XoUb5Phar3I/E8RAMDGJ/5nwCA1rBEZbrfNDU60YK8cD2tPPKocW3kUet2QQjxFqgmHfBroyZAxx8OP85myZhsHS1keZA3LpUAByUAme30cgBKGIbMj88tGGmtsmyBYJvk/HuqwzAKRG+Xvm+otflKm8dYEibEMrEFZFfAfKwkBLjgIVcaKTgOEiw864nGbBIIkqRrHz6PPm90T24a7ZqJLbcNT231222s2j1m7oHHIOxr0XZSvEb4s77JtqIhkjnzu3A3nSXg6Lfhc0mutozw6OEedFmNywG5m+xn2gVbjPF9ydrj90BWDn+u+Ptkrj011aUc+L62BcGVuX09G+bZ189ehWeXsdgJ/b618XFsvZUyrNJ4jGtejmW+8yDkSlOCnBycMEUhhLgNwKjjq/dIKf/VsR3AsVHg9oKm6v00AJTWPkdKX6WDcj5/EcfwWCCQ+6opzz2TEdNum7RGvq/U7iXuZ6btFHQFsjndtisI0PQLFMAupU2S7GtReqxrRWRnK7nqOfj9AXD6srmAtbO37HsgV50tXI0lEMcZS8XFLeW32ya1k99vyOY0bGfdGIv1elcshuabWw2cjoOPz3Y7cr94JpaiYyd2+nFXUJ+dm8+PPW8ETnni+i2Xs+LNew5sxW8fA3SveGlFT/eaWMfyGBY/r70A63UfXckS7TYOXnIJZjdvhhdFWPeIysyiuJBtRdtV3vx+Es8DKL0ZaRyML07oeeQLLZqrmU2bcu/hqCELi6InpJTXH8NhedS4NvKodZcECSC++uMC3c7aoJVmx4pRkHAoM/eItB5es0q1UkXtgj7a13xf6m5Zyn3V5Lqw3V/8WC5429VqfjFTqdT9ArEVOl+Fc2uJjzuTmsliLfb8EleRfXyecDFuqiTJ/Ea2b5wrbB7vsOMc/Pe0t3cqFaMoO5WKsmisbKrEGot9jszvwLYvJShcK+yjxXIFdGbBYyl6e18TwOYnIwGv/3TVPiz1e+ZtG3r6aaOgbWFt95Ug65S/SdxCoPeVnnG/3c7E4sjSowUXAMOIvGrvXgDAfuddHC2KGMWJgJMaN2c/F7XukqBc9U6cbXBPAcIuIWBV/PK0U+n7aLMKY5eJ70wjRbdJzYN19oNlMk/o2tZ5OOie+EtLPEJgAjWpVEweuedgVnWl53LqCYoheJpGJL2RtGDOLjjkSs24e6ysK1cwn7slSEHSdhHHmdRWOifNKZ8Hv93uKhBsV6vGEqR9aRVr/w68QM9lMdhxGdcYzELESoWWy1h1LhXMzYw1J/i7lHJw7Wtv4zEV1z556bwucGu0U6mgvn9/t9ItlbBYr+PwhRcCUJlmfZOTagHniNUlYZhpANUYHUV5bs7wSo089phuepRPlb9SEEXW07FDCPG/QXGgjwD4hhDiISnly3pR4wohPgPgUzqV1kmtuzSkcQ1F/f2Zh6kr2AxrtUvprFxgWwG9vAfMXuWTOS8sXyzPTLKD1ba7wz4/bS81m0rpWQ8nD8QC3a4ZPgZuDZA1YltbJFjJYqJxwrLW6H6N8mDJBEiSjPClfc35XMKIWVZUKMdTZjmxIlfOFKQnxUL3axfHEcg1YY6PIiAMjVXBt7ssF5+NoZebkW9fCkfrwuiVGn00wqursniZ41hKQfBxJWFo6mT2Xn21auuqMbRjEuHsrHlHiaadrGW6lvR9k1RCdS6V6WkMjI1lFjlxqYQgJ160kkpCn7FwPR0rpJRfBfDVnO/yqHF/i32eRA617lIg1xNfcdlV0q6HhX5sWo16iSJzo6Yz3Dqxaxu6BDtbldrFdJSGmvHn5twHrfZtwcmtgIAJQL5y5f53c2+MDI9bEdw8575hni5K982v5UznZS44nvnkCorS0Zm+4NZc8qpnfjy3QOha/F7Vl4kqmLPabXJ3E9rZuIbHlBvty11SHLZbMM8N5XpGVhI902iP4lgb9riPduXssqKDVgsjjz2G6S1bAACLW38EYBOSMDQ1LdHAQJflTBZqrKk6olHlPupUzlZps488Yo7xogjNkRH47fYJYYvNQMoimH26QUgtTMk9oV9i6fsms4MLWfJl2qsO4vDx223z8NmBXDovrSgzKYd65c2LkDLjtOodyBS34xi2G4QEURJnM0hiHXDlbhnheMG5YONC05j0zAJxWVLmXvVc2qysQJbbKvG8LmuLjucxnYyAdcQ+KKDM96XOcLxQjN8XALMqteFKK6WsLbuexv5N7GvxJAa+3bYulitkj1ehHO/q1hWb6bVvr6wiO2uQnufa+Lhx/z2z+gpMbdsDVLMRg/nzhlB7bIOxMogNoDkygvjcW7Bakxgeaf4VcO4n0Xny+pQZAcrSSMIQhy+8ECOPrSy/E4cogtmnH6TOqcq4E6AamZTn5lT+PBNQJEgW6/WMxUDHkZkLaAoGHQswLwdbVduCz4yJ+Wj5arxrJWv57v04NgV+mVW4FTOwV7H2CpCnyfrtlJyOWDf5ytlVFc2FNL+3TFyBnYssMr/dNtlGLoEi4ji7L1kESF88M2dsZUpWmq2AXePJVBWz7BeeQpwBU5R8vHnKl2IReVbEsaBXYPpEWiVHM15XHGQp8OeM2r0CANbfqtqrRkPA/Ga1rTUKBA00Lv2J2g6ofdbcpb7r34OAarS2vQO1b7wHIk6r6ikras/L1mPwEZHrElwZFMHs0w9CZFI8eRCyNThoqmZ5ER1l+nChxd1P5iHT/lLucvG0kLCzmGjlxIUTnZdbMXQOoDs90Pa/A6x62Frtc+Ft03vz1Tzds30M1ZPw/bhrJxNfQOre4+RylFXEhTXPauKuLR4Hsc/LfzfuduBCnfvm7TRKbukkSN1lXLG4MnnsjC272NCVveVK4VxJHM3q3s7kW875jhU0J4v1eob2xL4udz2RJd8aHMSRZz3LuI4QNFSfcgDw1JyXD1WwWB+BN3M2kuokvzAwdB/gRWjQb7X9/fCS7KKL4oDlsTVoV1tO9/GKYQWD2UKI3QDmoJLqOlLKy3vRGS2HDmm5OLMUhab8pWK1DOX19DQ87bPOpGVaFb28aCxmq+mM8LdWkC5COnM+/Td3TYk4Nit6TidBj1unUjF9ICjziM4Z+76p8QBSd1LieQiswKqdZsrdW9wFRat0we6N5tAWqtxNxueXu7cAlXXFlZRtlXBlSYoniLqryEWc7S9h5g/oSm+14SWJSZm03VeZ87B5tAWtcVMl+QyupwL4WH5aios6Obq+J9cjPWfTW7ZAxDGaIyMY2LMHhwfOVjsO66THyrjpskeLjna1Cn9WBa3jvo6yLmYvAoIGap5SIAvoXmBQAsSqvXsxPzRk4iHkglpJV9EJIAX8BSnlYfa3k87oKOiQloUzS1FA9TVOKhXVHY6vFjUvDefQsauyAZg0U1r9c5cSoWOt2oFuf2zmfMj2lojR7ZLiq2Nb8Rirg72U9vHGbdROqS7MeFn/iDyfOZ3ZFbAltKtVcz1SYjQ+LhSA7jiArTBiZBlrKSjPmWZ5DMgVWyHqCHus3EfO3WcuC4VbdLzS2pUCmkfD8bMKO9aSZ6lwihkgfR54/GuxXkdzdAhBU7k/a/tmAAALC69HvPEHwJHNqD6tGiI1N08jHmoAg7elzZK8SP0rjwPhFCbm1gNQ1of024gGBjB7lurP3T81ZehZVu3d2yUHVhQnPj02j85ouXRIy8IZpSiElJkqXvM/o3HoClyzwLP5G+kqudcjkOh0SpfPllY1nMaaVtI8XkEC1SaBI0bPzKoczEXF4h0k2Hgwm7t1uKKhcdm9jO06EhIMduCZE+RxU99WcjTXNFZ7xcsD+lwhBFw48fgKy36yM6mArKvIrnGwaxgyY2TbTrQr6VRG3j3bv1smRqdh13TwTD/u0kX/HqC5Hq3BQfPc18bHMVO5BgCwMEzEDZOAiIDpbep/AFh7u3I9AcpdtfO/AgAWR2exeMVN8B9+B1DfBQCYv+BrSqnsey3KYxeazCdvfBylOEZkMRAcF5bZuAjAGiHEA+zvT2tWiczZAPybEEIC+Gv9fR6d0XLpkJaFM0pRUCtUshIyvbKR5f2h/UhIdVVTs8waIPWt8wrqXqusqL8/I4BtRcAFGwl6e7VjKzWyigCWxhtFRtElnofAKqhL2LVIGHcqlUzmV2ApCQJP7wVS5UP9FmwXDK9VIYuBss0ycQXt7uKpvJSZxs/Hx2zGBGSsGh4/IasgUwdjKVszl45016WQF2g+3XCsitAVFKb3h7sSgVRZUAHs7AvvBSrj6GyewvT4DcCM6rtdPdAwzamSQdWyFH3jwMKo6tM9+JDa5kXoW/UTLMQ+6kGCyiX/HQCwJghQ833cP7TPtG39i/Mk/u+xMSyc+2ksbhxC/ODvAUgbGfUiUzxaiOWzxx5eRuOiq6WUY1oZfEcIsaPXpR3bjpkO6YxSFBCp4OW0FiRcbIEhvG6KZ9s85a4Jv9025rU5BzNrOSrT0ybWAKSrV8o64umgxnXDKoopjsHHbLcgpc8UYJe+bwqR+qemTHEe358ovvlq3nzWLiy6X+haEgIpmKDVygoGUmiO7Cgbropw2p9+I552y90YmfHmZRrxuhM2DlcA+2iwnMDy6aA8jsdaooWRnSZs37fLEl2/8XYcOLQNGHsl0NwM6J7kC8PD+jmKgbbOcPIjlQFVaqRWxPQ2tKpPAfPnYK5Tw6vP3QcAGA0C3Dgxgcsu+wQePKjiHg8tHMLN55yDuxoN3Do7hkcu+4Q6x/ZjKs1aAiuX9SSlHNP/HxJCfBXKlZRHZ7RcOqRl4YxSFFKoXtkU5OSpjmaFbaWbmmMtX2zMrA7aThaGXWTlt9vZ3smssM2mseaVybQPpbzarhjjt2cFb4C2TphridxJnLobgOkWxxUM75lB90cuKwrWA6lLisc6KLBMysfuHMYtIKOMLLcEzS8PUpvjXNlPSZKZb7IYbOZW2j9juR2F1WC7Je3jXFlPpzpWerx2IoSM07oaHqNarNfNtSnjaOb+P1eCPw6BdbebcyYiQrjjlwEA/Yfo2ayjU5lR6bGHr9E3E0G2RlE//1O4slrFv0yrfece/RNgYDseXHs7XrdZ9Z4I4OGWmRmsCQI8cmiLCpRD9RFf98gjKysUV6iOQghRBeBJKef055cC+ADy6YyWS4e0LJxRikJIaYK6vAaCr2IBZPymdsDaLhbiq6bE8zIstPRi0EvCr+cBCGZnu/zenBuKtttCiFbNdnCWejfza8s4bUdpn8dkE3FiQ+035qtuviKk2AWvjOX3SdtsWm9jWdG8gQXCLeVsu+x4+q/d+5ioprnyFXGMUBe68ZeUz+tyYKckA8pVt0yf8ymJE63M7OeSFin8GaCWqXGppHpHAKhOTKTUG09cZuZ95qIOogGBNY8+00XhMXT3JrQGVdA78Tzg8Ca0d30Qt7O2w36pBDE5jM7kFfjy2HY1yNFb8ctrWzjc6UDUH4d84FN6XHsx9rznpb/vl1ZkRlZqztcB+Kru4RMAuElKeasQ4n446Ix60SEdC84oRQGZ1jVk3DPMF+4xdwq5ezJ8Pnq1Sit8blG4OH+AVGib1p4szdMODic0Dus8frttAufG70v+fasYzfYF+0jdRlzRGYoMdi3bUjCWjh4zWRxkJXAxyq0e7hJzuVyo6ImPH0gtIA5yMZkeIFZ1tM1Zxc91NC+pvQjIWJqOhYG572VewxWzyjv2dHBT2TBuPNrA3yW2Hyl4u/6lsXkz6vv3Z9zCpfsr8JJdxqKl65DVSB3qeEOxxVbLvGutwUH9rlQRRVel11rzFTwwPw/ZfBbw7I8AAGYvfwqDvo93rFsHAHjvH67AnKxQ1pOU8mkAlzq259IZ5dEhHQvOLEUBkfq5uSvIS3s18JeZ/88fdHLhxIAh3+PKxxYiXhRlAsS0na9w6RhyERG4oO9yfwGZtqX2OOh8ZuWN7pfZTgs1RX+WuWynkLpW/Jx5kwtZmyfKzKkOXGf2ZTEE/oJlCOR68BXx3+9Yg9GUeUZzzL93ubSO9hrLcVP1SoRY6rhe+Gm4yGzrl/i0+Peen6V795LEWBdBq2UIO3lwmazZTqVi2GPpnSIeKGp/S4sNep6jDU+ZYPZlqxaxL9Jj7NTUPwCyMo7Bcgc7FxdXbjKWn/V0SuMMUxRZXnuepsebFtlcPTzfmzJ66PtMqp8VsPaiCNSD2ksS86DHUYRwfl7VS7DsJE/72zO9HGiV3m5nsoqo8I+ELY3H0/GTDOU10gI7uwiOCunM3FiZTGZOoKktLPoLO3AeMJePERh6TjPKJYpy+zbbAWYerLazwyi4bbuujhb8N6ZzcLca97Uf77WOxgJZafw0lIS9UOJ8TEA23mcsDuaaFHGMcpzNRPTbbUA//+W5ObPwondqsV43zx+vCBdxjPD6d+N5lQquqSmFMB37+P8PxCpwnoTAxn8CAJSCeeyLgC/szm2YefQoemafhtAJY2SimmCpJRB4wZwrm4lcM7bpDGRrBoAsE6u9TVYqmeAxt2gEe1EIPBbhIa0J4P0VeKqruR5SZcHjMVxBAim3FafUoAwVW3i7VrsmiKwD8JzeghMV8nkAtCVjFSkmnpetd3DEWPi8HSu4u8mOVXFBZhIIfgaYQE8k8qwgOzON3JbcipM6thT195tnutRsQlYqaOm+IdDHtAYHMXPOGvzyz78PAPA7IyN4+Td+BeHBdYjOuR+dfT9nrrX4w4+icdWf4KMHD6ptz7wR2HwTRp71RVxereKeRgMA0JICC3Pn4Bc3quSgb63AfAgUpICnJSiuwIUWCUd7xUMPNLcyZByb9qS85wM/L3+guSuFlAIJbE9TeJvjAXiWMKQMoowfn4SWXm3x2AWQVS6GII8JbSBbNc7dSfa1qNmRKxBMq2x+fVdcwFXtSu48v92Gj24iPrvKmcc8XDiWmAF3N3ZRqDjO+bOwMvxpwHaRupI57LnMs9TIdcTjZrJSQf+v/jn+aO1ajAYq3TsQAs++9ON4fCEGDl2HePRhfeIQ1176Odx58Kw0lXbjP2F1kGBbfxXX1+vYqBdyW8tldNa3MN4ur+BkFBbFaQcpRBcJGQDDYcSJ+QDtmtJC0i64cwUleT0GAFP3ELbbWeGN1O3lLKJD9mWj6+VZL7b7h3iYgCyJYebYMExbQ3ISQ4tPiVdX202NKD3VngdX1pLdD6KrWJBZKq4YxVJYaRfQcoPOBVLYc2a7cV3K3352TdMqWtjohQrnIYtLJRx4+rVorbkD0/qcj87O4vFdL1H1FbWdQDilTtqp4c6D63DZyAHs08/g9QMDaMQBBoMANx85gtevXg0AGC2VUPM8rAlWUiwWiuK0g5BpwVxGoOv+EgmLFwAqUE2peHy1blahzAqhFROt9AF0uWA4OHU232YriIwflwl089KwTCQKwPLguy2keUyFruGipuCprnSfnBGWZ57YK0GaCy4kbLeR6175OU42ToUxnK4wz9VRJBZQJT4tfvomFakfUe4kAKaer57zvvM+iQ+uX49bZ+bwgI5/LN5zI0KysI9cAqx+RJ04DoH9r8SD+JqiCAFw2+wsbj3vPGwJQ4x3Onh0YQEA0JESfz81hS/vvGjl5uJnJJgtpDzmqu7TDkKICQDPnMBLrAFweMm9Tm0U93BqoLiHk4+zpZQjx3MCIcStUPOwFA5LKW84nmudSJxRiuJEQwjxwDL4Wk5pFPdwaqC4hwKnEo6ugW6BAgUKFDjjUCiKAgUKFCjQE4WiWFnY/PGnI4p7ODVQ3EOBUwZFjKJAgQIFCvREYVEUKFCgQIGeKBTFMUIIsUkI8R9CiMeFEI8JId7Ovvs9IcRP9PY/P5nj7IW8exBCbBNC3COEeEgI8YAQ4oqTPdY8CCEqQoj7hBA/1vfwfr19SAjxHSHEk/r/1Sd7rHnocQ8fEULsEEI8LIT4qhBi8GSP1YW88bPv/0AIIYUQy0kTLXAKonA9HSN0N6n1UsofCSHqAH4I4NVQvPHvAfByKeWiEGKtlPJQr3OdLPS4h/8B4GNSym8JIX4JwB9JKV90EoeaC6EI+qtSyoYQogTgLgBvB/AaAFNSyg8JId4NYLWU8l0nc6x56HEPAwBul1J2hBAfBoBT8R7yxi+lvEcIsQnAZwBcCOD5UsrTua7ijEVhURwjpJQHpJQ/0p/nADwO1bz8rQA+JKVc1N+dkkoC6HkPEkpIAcAqHEcLxRMNqdDQf5b0PwngVQA+p7d/DkoBnpLIuwcp5b9JKTt6+z1Q7SxPOfT4DQDgYwD+iP1d4DREoShWAEKILQAuA3AvgPMBXCuEuFcI8V0hxAtO5tiWC+se3gHgI0KIvQA+CuCPT97IloYQwhdCPATVL/g7Usp7AayTUh4AlEIEsILc0SuPnHvg+D+xMoSmJwSu8QshXglgv5Tyxyd5eAWOE4WiOE4IIWoA/hnAO6SUs1D8WasBXAngD6HaFIqTOMQl4biHtwJ4p5RyE4B3Avibkzm+pSCljKWU26BW3FcIIS4+2WM6WvS6ByHEe6DaWX7xZI1vKTjG/1woF+yfntyRFVgJFIriOKD9sf8M4ItSyq/ozfsAfEWb4/dBtYI4ZYN4OffwRgD0+csATtlgNoeUchrAHQBuAHBQx2AoFnPKugA5rHuAEOKNAF4B4A3yNAgosvG/CsA5AH4shNgNpUB+JIQYPXmjK3CsKBTFMUJbCX8D4HEp5V+yr/4FwHV6n/MBhDhFidF63MMYgJ/Xn68D8ORPe2zLhRBihLKBhBB9AK4HsAPA16AUHvT//3pyRrg08u5BCHEDgHcBeKWUcv5kjrEXcsb/oJRyrZRyi5RyC9QC6nlSyvGTONQCx4gzimZ8hXE1gP8DwCPaNwsAfwLgbwH8rRDiUZJGm/IAAAMLSURBVAARgDeewivBvHv4bQAfF0IEAFoA3nKSxrccrAfwOSGED7Xw+ZKU8hYhxN1Qbr83A9gD4HUnc5BLIO8edgIoA/iO9l7eI6X8nZM4zjw4x3+Sx1RgBVGkxxYoUKBAgZ4oXE8FChQoUKAnCkVRoECBAgV6olAUBQoUKFCgJwpFUaBAgQIFeqJQFAUKFChQoCcKRVHglIcQorH0Xsd1/s8IIS7Sn//kGI7fotOhCxT4mUSRHlvglIcQoiGlrJ2q19I8WbdIKU876pACBZaDwqIocFpCCHG2EOLfda+GfxdCbNbbPyuE+CshxA+EEE8LIV6rt3tCiP+p+yXcIoT4JvvuDiHE5UKIDwHoE6oPxxdtS0H3VXif/vx83X/hbgC/y/bxdR+J+/XY/stPcVoKFDghKBRFgdMVNwL4vJTyuVBkeX/FvlsP4BoojqQP6W2vAbAFwCUAfgvAVfYJpZTvBrAgpdwmpXzDEtf/OwBvk1La53kzgBkp5QsAvADAbwshzjmaGytQ4FRDoSgKnK64CsBN+vMXoBQD4V+klImUcjtUIyno77+st48D+I9jvbAQYhWAQSnld9n1CS8F8BuaEuVeAMMAzjvWaxUocCqg4Hoq8LMCHmxbZJ+F9f/RoIPsYqrCzpUX3BMAfk9K+e1juF6BAqckCouiwOmKHwB4vf78Bqj2m71wF4Bf0bGKdQBelLNfW1OvA8BBAGuFEMNCiDKUK4uotGeEEGTFcDfVtwG8lc4hhDhfCFE9ivsqUOCUQ2FRFDgd0C+E2Mf+/ksAb4Ni6f1DABMA3rTEOf4ZwIsBPArgCSi30Ixjv08DeFgI8SMp5RuEEB/Q++6Coi8nvElffx5KORA+AxUL+ZGmcZ/AKdyGtUCB5aBIjy1wxkAIUZNSNoQQwwDuA3B10R+hQIGlUVgUBc4k3KIb7IQA/qxQEgUKLA+FRVGgQIECBXqiCGYXKFCgQIGeKBRFgQIFChToiUJRFChQoECBnigURYECBQoU6IlCURQoUKBAgZ4oFEWBAgUKFOiJ/wWOGbppFEHqRwAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ "<Figure size 432x288 with 2 Axes>"
+ ]
+ },
+ "metadata": {
+ "needs_background": "light"
+ },
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.pcolormesh(lon, lat, altitude, cmap='terrain')\n",
+ "plt.ylabel('Latitude')\n",
+ "plt.xlabel('Longitude')\n",
+ "plt.colorbar()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "### Describing the geometry\n",
+ "\n",
+ "This section describe transformation functions that we will need to construct our manifold.\n",
+ "\n",
+ "The following two functions then define the forward and inverse\n",
+ "transformations that correspond to the WGS 84 reference shape of\n",
+ "Earth. The forward transform follows the formula shown in the\n",
+ "introduction. The inverse transform is significantly more complicated\n",
+ "and is, at the very least, not intuitive. It also suffers from the\n",
+ "fact that it returns an angle that at the end of the function we\n",
+ "need to clip back into the interval $[0,2\\pi]$ if it should have\n",
+ "escaped from there."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "R = 6378137\n",
+ "ellipticity = 8.1819190842622e-2\n",
+ "r2d = 180. / math.pi\n",
+ "d2r = math.pi / 180.\n",
+ "\n",
+ "def push_forward_wgs84(phi_theta_d):\n",
+ " phi = phi_theta_d[0]\n",
+ " theta = phi_theta_d[1]\n",
+ " d = phi_theta_d[2]\n",
+ "\n",
+ " R_bar = R / math.sqrt(1. - (ellipticity**2. *\n",
+ " math.sin(theta) * math.sin(theta)))\n",
+ "\n",
+ " return [(R_bar + d) * math.cos(phi) * math.cos(theta),\n",
+ " (R_bar + d) * math.sin(phi) * math.cos(theta),\n",
+ " ((1. - ellipticity**2.) * R_bar + d) * math.sin(theta)]\n",
+ "\n",
+ "def pull_back_wgs84(x):\n",
+ " b = math.sqrt(R * R * (1 - ellipticity * ellipticity))\n",
+ " ep = math.sqrt((R * R - b * b) / (b * b))\n",
+ " p = math.sqrt(x[0]**2. + x[1]**2.)\n",
+ " th = math.atan2(R * x[2], b * p)\n",
+ " phi = math.atan2(x[1], x[0])\n",
+ " theta = math.atan2(x[2] + ep * ep * b * math.pow(math.sin(th), 3.),\n",
+ " (p -\n",
+ " (ellipticity * ellipticity * R * math.pow(math.cos(th), 3))))\n",
+ " R_bar = R / (math.sqrt(1 - ellipticity * ellipticity * math.sin(theta) *\n",
+ " math.sin(theta)))\n",
+ " R_plus_d = p / math.cos(theta)\n",
+ "\n",
+ " phi_theta_d = [0, 0, 0]\n",
+ " if phi < 0:\n",
+ " phi_theta_d[0] = phi + 2 * math.pi\n",
+ " elif phi > 2 * math.pi:\n",
+ " phi_theta_d[0] = phi - 2 * math.pi\n",
+ " else:\n",
+ " phi_theta_d[0] = phi\n",
+ " phi_theta_d[1] = theta\n",
+ " phi_theta_d[2] = R_plus_d - R_bar\n",
+ " \n",
+ " return phi_theta_d"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Next, the topography transformations follow exactly the description in the introduction. The only thing to note here is that we invoke the interpolant for the input topography data that we constructed above:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def push_forward_topo(phi_theta_d_hat):\n",
+ " d_hat = phi_theta_d_hat[2]\n",
+ " h = topo_function((phi_theta_d_hat[1]*r2d, phi_theta_d_hat[0]*r2d))\n",
+ " d = d_hat + (d_hat + 500000.) / 500000. * h\n",
+ " \n",
+ " return [phi_theta_d_hat[0], phi_theta_d_hat[1], d]\n",
+ "\n",
+ "def pull_back_topo(phi_theta_d):\n",
+ " d = phi_theta_d[2]\n",
+ " h = topo_function((phi_theta_d[1]*r2d, phi_theta_d[0]*r2d))\n",
+ " d_hat = 500000. * (d - h) / (500000. + h)\n",
+ " \n",
+ " return [phi_theta_d[0], phi_theta_d[1], d_hat]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Finally, both of the pull back and push forward functions are just concatenations of the respective functions of the WGS 84 and topography mappings:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def pull_back(space_point):\n",
+ " return pull_back_topo(pull_back_wgs84(space_point))\n",
+ "\n",
+ "def push_forward(chart_point):\n",
+ " return push_forward_wgs84(push_forward_topo(chart_point))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Now we are ready to construct a FunctionManifold object with the defined transformations:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "geometry = dealii.Manifold(dim = 3, spacedim = 3)\n",
+ "geometry.create_function(push_forward, pull_back)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "### Creating the mesh"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Having so described the properties of the geometry, not it is\n",
+ "time to deal with the mesh used to discretize it. To this end,\n",
+ "we create objects for the geometry and triangulation, and then\n",
+ "proceed to create a $1\\times 2\\times 1$ rectangular mesh that\n",
+ "corresponds to the reference domain\n",
+ "$\\hat U=[26,35]\\times[-10,5]\\times[-500000,0]$. We choose\n",
+ "this number of subdivisions because it leads to cells that\n",
+ "are roughly like cubes instead of stretched in one direction or\n",
+ "another.\n",
+ "\n",
+ "Of course, we are not actually interested in meshing the\n",
+ "reference domain. We are interested in meshing the real domain.\n",
+ "Consequently, we will use the GridTools::transform() function\n",
+ "that simply moves every point of a triangulation according to\n",
+ "a given transformation. The transformation function it wants is\n",
+ "a function that takes as its single argument a point in the reference\n",
+ "domain and returns the corresponding location in the domain that we\n",
+ "want to map to. This is, of course, exactly the push forward\n",
+ "function of the geometry we use. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "triangulation = dealii.Triangulation('3D')\n",
+ "triangulation.generate_subdivided_hyper_rectangle(repetitions = [1, 2, 1],\\\n",
+ " p1 = dealii.Point([26 * d2r, -10 * d2r, -500000]),\\\n",
+ " p2 = dealii.Point([35 * d2r, 5 * d2r, 0.]), colorize = True)\n",
+ "\n",
+ "triangulation.transform(push_forward)\n",
+ "\n",
+ "manifold_id = 0\n",
+ "\n",
+ "triangulation.set_manifold(number = manifold_id, manifold = geometry)\n",
+ "for cell in triangulation.active_cells():\n",
+ " cell.set_all_manifold_ids(manifold_id) "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ " The last step is to refine the mesh beyond its initial $1\\times 2\\times\n",
+ " 1$ coarse mesh. We could just refine globally a number of times, but\n",
+ " since for the purpose of this tutorial program we're really only\n",
+ " interested in what is happening close to the surface, we just refine 6\n",
+ " times all of the cells that have a face at a boundary with indicator 5.\n",
+ " Looking this up in the documentation of the\n",
+ " GridGenerator::subdivided_hyper_rectangle() function we have used above\n",
+ " reveals that boundary indicator 5 corresponds to the top surface of the\n",
+ " domain (and this is what the last <code>True</code> argument in the call\n",
+ " to *generate_subdivided_hyper_rectangle()* above meant: to \"color\"\n",
+ " the boundaries by assigning each boundary a unique boundary indicator)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "for n in range(6):\n",
+ " for cell in triangulation.active_cells():\n",
+ " for face in cell.faces():\n",
+ " if face.at_boundary() and face.boundary_id == 5:\n",
+ " cell.refine_flag ='isotropic'\n",
+ " \n",
+ " triangulation.execute_coarsening_and_refinement()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Let us now print some statistics about our mesh:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "# of cells = 19112\n",
+ "smallest cell = 21579.0 m\n",
+ "largest cell = 660950.0 m\n"
+ ]
+ }
+ ],
+ "source": [
+ "print('# of cells = %d\\nsmallest cell = %0.1f m\\nlargest cell = %0.1f m' % (triangulation.n_active_cells(),\\\n",
+ " triangulation.minimal_cell_diameter(),\\\n",
+ " triangulation.maximal_cell_diameter()))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "We can finally save the mesh:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "triangulation.write('mesh.vtu', 'vtu')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "This gives us the following mesh (here coloured by the element volume):\n",
+ "\n",
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "For details about visualization and discussionof results and underlying issues the reader is referred to the section [Results](https://www.dealii.org/current/doxygen/deal.II/step_53.html) of the original tutorial program."
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.7.3"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}